Does anyone know how to solve $$\int_a^b \frac{1}{x}\sqrt{-(x-a)(x-b)}dx$$ After trying Wolfram Alpha, I conclude that it possibly equals $(\frac{a+b}{2}-\sqrt{ab})\pi = \frac{(\sqrt{a}-\sqrt{b})^2}{2}\pi$. The book I am reading says one can use residue theorem to quickly obtain the result, but the details are not written and I cannot figure out the solution.
P.S. One can prove from this integral that arithmetic mean $\geq$ geometric mean.
Strip units under the radical. $x-a=(b-a)t$ $$I=\int_a^b\frac1x\sqrt{(x-a)(b-x)}dx=(b-a)^2\int_0^1\frac{\sqrt{t(1-t)}}{a+(b-a)t}dt$$ Then a trig substitution to eliminate the radical. $t=\sin^2\theta$ $$I=2(b-a)^2\int_9^{\pi/2}\frac{\sin^2\theta\cos^2\theta}{a+(b-a)\sin^2\theta}d\theta$$ Then an inverse trig substitution, to reduce the integrand to a rational function, $u=\tan\theta$ $$\begin{align}I&=2(b-a)^2\int_0^{\infty}\frac{u^2}{(1+u^2)^2(a+bu^2)}du\\ &=2\int_0^{\infty}\left(\frac{b-a}{(1+u^2)^2}+\frac a{1+u^2}-\frac{ab}{a+bu^2}\right)du\end{align}$$ If we let $u=\tan\theta$ again we get $$\begin{align}2\int_0^{\infty}\left(\frac{b-a}{(1+u^2)^2}+\frac a{1+u^2}\right)du&=2\int_0^{\pi/2}\left((b-a)\cos^2\theta+a\right)d\theta\\ &=2\frac{\pi}2\left(\frac12(b-a)+a\right)=\frac{\pi}2(b+a)\end{align}$$ Because the average value of $\cos^2\theta$ is $1/2$, the average value of $1$ is $1$ and the length of the interval is $\pi/2$. Then in the last integral we can let $\sqrt b\,u=\sqrt a\,\tan\phi$ so $$-2ab\int_0^{\infty}\frac{du}{a+bu^2}=-2\sqrt{ab}\int_0^{\pi/2}d\phi=-\pi\sqrt{ab}$$ Adding up, we get $$I=\int_a^b\frac1x\sqrt{(x-a)(b-x)}dx=\pi\left(\frac{b+a}2-\sqrt{ab}\right)$$ But did you want the residue theorem?
EDIT: Since the answer was in the affirmative, we note first that there is a problem that the integrand approaches $1$ as $|x|\rightarrow\infty$. Thus the closure of the contour is problematic. Accordingly I make the substitution $t=1/x$:
$$\int_a^b\frac{\sqrt{(x-a)(b-x)}}xdx=\int_{1/b}^{1/a}\frac{\sqrt{(1-at)(bt-1)}}{t^2}dt$$
Now we can do some contour integratin'! Consider the contour $C$ illustrated below that starts on the right edge of a circle of radius $r$ centered at $z=1/a$, goes due east along contour $C_1$ until it hits a circle of radius $R$ centered at $z=0$, follows that circle counterclockwise along contour $C_2$ until it's back at the real axis again, goes back west along contour $C_3$ until it again encounters the circle of radius $r$ centered at $z=1/a$, follow that circle clockwise along contour $C_4$ until it hits the real axis west of $z=1/a$, follows the real axis west along contour $C_5$ until it encounters the circle of radius $r$ centered at $z=1/b$, follows that circle clockwise along contour $C_6$ until it hits the real axis east of $z=1/b$, goes east along contour $C_7$ until it encounters the circle of radius $r$ centered at $z=1/a$ and finally follows that circle clockwise along contour $C_8$until it arrives back at its starting point.
Contours $C_4$, $C_6$, and $C_8$ contribute nothing to the integeral as $r\rightarrow0$ because the magnitudes of the integrand are bounded there and the length of the contours approaches zero. Contours $C_1$ and $C_3$ have the same phase because we take the branch cut from $z=1/b$ to $z=1/a$ along the real axis. They are traversed in opposite directions, however, so the cancel. Contour $C_7$ is the integral we want and this time contour $C_5$ has opposite phase and direction so it has the same magnitude and sign as contour $C_7$. Contour $C_2$ is the formerly problematic closure
$$\begin{align}\int_{C_2}\frac{\sqrt{(1-az)(bz-1)}}{z^2}dz&=\int_0^{2\pi}\frac{\sqrt{(1-aRe^{i\theta})(bRe^{i\theta}-1)}}{R^2e^{2i\theta}}iRe^{i\theta}d\theta\\
&=\int_0^{2\pi}i\sqrt{ab}e^{-\pi i/2}\left(1+O(1/R)\right)d\theta\\
&=2\pi\sqrt{ab}+O(1/R)\rightarrow2\pi\sqrt{ab}\end{align}$$
As $R\rightarrow\infty$ We thus have the results
$$2\int_a^b\frac{\sqrt{(x-a)(b-x)}}xdx+2\pi\sqrt{ab}=2\pi i\sum(\text{residues})$$
The only pole within the contour is at $z=0$ and it's a second-order pole, so
$$\begin{align}\sum(\text{residues})&=\left.\frac d{dz}\left(z^2\frac{\sqrt{(1-az)(bz-1)}}{z^2}\right)\right|_{z=0}\\
&=\left.-\frac a2\frac{\sqrt{bz-1}}{\sqrt{1-az}}+\frac b2\frac{\sqrt{}1-az}{\sqrt{bz-1}}\right|_{z=0}\end{align}$$
Now, at this pole the phase of $1-az$ is zero but the phase of $bz-1$ is $\pi$ so $\sqrt{bz-1}=e^{\pi i/2}$ and
$$\sum(\text{residues})=-\frac a2e^{\pi i/2}+\frac b2e^{-\pi i/2}=-\frac i2(a+b)$$
So we are done:
$$\int_a^b\frac{\sqrt{(x-a)(b-x)}}xdx=-\pi\sqrt{ab}+\frac{\pi}2(a+b)$$
Was that really easier?
EDIT: Of course after typesetting all this stuff and drawing the figure and submitting it I could see how to do the contour integral without any substitutions. The contour is the same as in my illustration except that the point $z=1/b$ becomes $z=a$ and the point $z=1/a$ becomes $z=b$. The 'problematic' closure contour $C_2$ is handled by observing that $$\begin{align}\sqrt{Re^{i\theta}-a}&=\sqrt Re^{i\theta/2}\sqrt{1-\frac aRe^{-i\theta}}\\ &=\sqrt Re^{i\theta/2}\left\{1-\frac a{2R}e^{-i\theta}-\frac{\frac{a^2}{4R^2}e^{-2i\theta}}{\sqrt{1-\frac aRe^{-i\theta}}+1-\frac a{2R}e^{-i\theta}}\right\}\end{align}$$ And $$\begin{align}\sqrt{b-Re^{i\theta}}&=\sqrt Re^{i\theta/2}e^{-\pi i/2}\sqrt{1-\frac bRe^{-i\theta}}\\ &=\sqrt Re^{i\theta/2}e^{-\pi i/2}\left\{1-\frac b{2R}e^{-i\theta}-\frac{\frac{b^2}{4R^2}e^{-2i\theta}}{\sqrt{1-\frac bRe^{-i\theta}}+1-\frac b{2R}e^{-i\theta}}\right\}\end{align}$$ Then after multiplying everything out and noting also that $$\int_0^{2\pi}Re^{i\theta}d\theta=\int_0^{2\pi}R^{-1}e^{-i\theta}d\theta=0$$ We get useful stuff from contour $C_2$ after all.
Let $\sin^2t = \frac{x-a}{b-a}$
\begin{align} &\int_a^b \frac{1}{x}\sqrt{(a-x)(x-b)}dx \\ =& \int_0^{\pi/2} \frac{{(b-a)^2}(1-\cos^2 2t)}{(a+b)-(b-a)\cos 2t}\>dt\\ =&\int_0^{\pi/2} \left[(a+b) + (b-a)\cos2t - \frac{4ab}{(a+b)-(b-a)\cos 2t} \right]dt\\ =& \frac{(a+b)\pi}2 - \sqrt{ab}\pi \\ \end{align} where $\int_0^{\pi/2} \frac{du}{p-q\cos2t}=\frac{\pi}{2\sqrt{p^2-q^2}}$ is used.
Let $x=a\cos^2 t+b \sin^2 t \implies dx=(b-a) \sin 2t dt$
Then $$I=2\int_{0}^{\pi/2} \frac{(b-a)^2 \sin^2 t \cos^2 tdt}{a \cos^2 t+b \sin^2t}= 2 (b-a)^2 \int_{0}^{\pi/2}\frac{ \sin^2 t ~dt}{a+b\tan^2 t}$$
Let $\tan t=u$, then
$$I=2\int_{0}^{\infty} \frac{u^2 du}{(1+u^2)^2(a+bu^2)}=2\int_{0}^{\infty} du \left(\frac{b-a}{(1+u^2)^2}+\frac{a}{1+u^2}-\frac{ab}{a+bu^2}\right)$$
$$\implies I=\left. (b-a)\left(\frac{u}{1+u^2}+\tan^{-1}u\right)+2a \tan^{-1}u -2\sqrt{ab} ~\tan^{-1}\frac{u\sqrt{b}}{\sqrt{a}} \right|_{0}^{\infty}=\left(\frac{a+b}{2}-\sqrt{ab} \right) \pi $$
I will get back.
Let $n\in\mathbb{N}=\{1,2,\dotsc\}$ and $\boldsymbol{a}=(a_1,a_2,\dotsc,a_n)$ be a positive sequence, that is, $a_k>0$ for $1\le k\le n$. The arithmetic and geometric means $A_n(\boldsymbol{a})$ and $G_n(\boldsymbol{a})$ of the positive sequence $\boldsymbol{a}$ are defined respectively as \begin{equation*} A_n(\boldsymbol{a})=\frac1n\sum_{k=1}^na_k \quad \text{and}\quad G_n(\boldsymbol{a})=\Biggl(\prod_{k=1}^na_k\Biggr)^{1/n}. \end{equation*} For $z\in\mathbb{C}\setminus(-\infty,-\min\{a_k,1\le k\le n\}]$ and $n\ge2$, let $\boldsymbol{e}=(\overbrace{1,1,\dotsc,1}^{n})$ and \begin{equation*} G_n(\boldsymbol{a}+z\boldsymbol{e})=\Biggl[\prod_{k=1}^n(a_k+z)\Biggr]^{1/n}. \end{equation*}
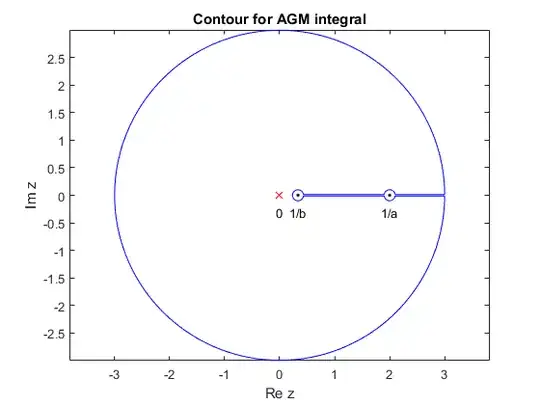
In Theorem 1.1 of the paper [1] below, by virtue of the Cauchy integral formula in the theory of complex functions, the following integral representation was established.
Theorem 1.1. Let $\sigma$ be a permutation of the sequence $\{1,2,\dotsc,n\}$ such that the sequence $\sigma(\boldsymbol{a})=\bigl(a_{\sigma(1)},a_{\sigma(2)},\dotsc,a_{\sigma(n)}\bigr)$ is a rearrangement of $\boldsymbol{a}$ in an ascending order $a_{\sigma(1)}\le a_{\sigma(2)}\le \dotsm \le a_{\sigma(n)}$. Then the principal branch of the geometric mean $G_n(\boldsymbol{a}+z\boldsymbol{e})$ has the integral representation \begin{equation}\label{AG-New-eq1}\tag{1} G_n(\boldsymbol{a}+z\boldsymbol{e})=A_n(\boldsymbol{a})+z-\frac1\pi\sum_{\ell=1}^{n-1}\sin\frac{\ell\pi}n \int_{a_{\sigma(\ell)}}^{a_{\sigma(\ell+1)}} \Biggl|\prod_{k=1}^n(a_k-t)\Biggr|^{1/n} \frac{\textrm{d}\,t}{t+z} \end{equation} for $z\in\mathbb{C}\setminus(-\infty,-\min\{a_k,1\le k\le n\}]$.
Taking $z=0$ in the integral representation \eqref{AG-New-eq1} yields \begin{equation}\label{AG-ineq-int}\tag{2} G_n(\boldsymbol{a})=A_n(\boldsymbol{a})-\frac1\pi\sum_{\ell=1}^{n-1}\sin\frac{\ell\pi}n \int_{a_{\sigma(\ell)}}^{a_{\sigma(\ell+1)}} \Biggl[\prod_{k=1}^n|a_k-t|\Biggr]^{1/n} \frac{\textrm{d}\,t}{t}\le A_n(\boldsymbol{a}). \end{equation} Taking $n=2,3$ in \eqref{AG-ineq-int} gives $$ \frac{a_1+a_2}{2}-\sqrt{a_1a_2}\,=\frac1\pi\int_{a_1}^{a_2} \sqrt{\biggl(1-\frac{a_1}{t}\biggr) \biggl(\frac{a_2}{t}-1\biggr)}\, \textrm{d}\,t\ge0 $$ and $$ \frac{a_1+a_2+a_3}{3}-\sqrt[3]{a_1a_2a_3}\, =\frac{\sqrt{3}\,}{2\pi} \int_{a_1}^{a_3} \sqrt[3]{\biggl| \biggl(1-\frac{a_1}{t}\biggr) \biggl(1-\frac{a_2}{t}\biggr) \biggl(1-\frac{a_3}{t}\biggr)\biggr|}\,\textrm{d}\,t\ge0 $$ for $0<a_1\le a_2\le a_3$.
Weighted version of the integral representation \eqref{AG-New-eq1} can be found in the paper [2] below. We recite the weighted version as follows.
For $n\ge2$, $\boldsymbol{a}=(a_1,a_2,\dotsc,a_n)$, and $\boldsymbol{w}=(w_1,w_2,\dotsc,w_n)$ with $a_k, w_k>0$ and $\sum_{k=1}^nw_k=1$, the weighted arithmetic and geometric means $A_{w,n}(\boldsymbol{a})$ and $G_{w,n}(\boldsymbol{a})$ of $\boldsymbol{a}$ with the positive weight $\boldsymbol{w}$ are defined respectively as \begin{equation} A_{\boldsymbol{w},n}(\boldsymbol{a})=\sum_{k=1}^nw_ka_k \end{equation} and \begin{equation} G_{\boldsymbol{w},n}(\boldsymbol{a})=\prod_{k=1}^na_k^{w_k}. \end{equation} Let us denote $\alpha=\min\{a_k,1\le k\le n\}$. For a complex variable $z\in\mathbb{C}\setminus(-\infty,-\alpha]$, we introduce the complex function \begin{equation}\label{complex-geometric-mean} G_{\boldsymbol{w},n}(\boldsymbol{a}+z)=\prod_{k=1}^n(a_k+z)^{w_k}. \end{equation} In Section 3 of the paper [2] below, with the aid of the Cauchy integral formula in the theory of complex functions, the following integral representation was established.
Theorem 3.1. Let $0<a_k\le a_{k+1}$ for $1\le k\le n-1$ and $z\in\mathbb{C}\setminus(-\infty,-a_1]$. Then the principal branch of the weighted geometric mean $G_{\boldsymbol{w},n}(\boldsymbol{a}+z)$ with a positive weight $\boldsymbol{w}=(w_1,w_2,\dotsc,w_n)$ has the integral representation \begin{equation}\label{AG-New-eq1-weighted}\tag{3} G_{\boldsymbol{w},n}(\boldsymbol{a}+z)=A_{\boldsymbol{w},n}(\boldsymbol{a})+z-\frac1\pi\sum_{\ell=1}^{n-1}\sin\Biggl[\Biggl(\sum_{k=1}^{\ell}w_k\Biggr)\pi\Biggr] \int_{a_\ell}^{a_{\ell+1}} \prod_{k=1}^n|a_k-t|^{w_k} \frac{\textrm{d}\,t}{t+z}. \end{equation} Letting $z=0$ in the integral representation \eqref{AG-New-eq1-weighted} gives \begin{equation}\label{AG-New-eq1-weighted-z=0}\tag{4} G_{\boldsymbol{w},n}(\boldsymbol{a})=A_{\boldsymbol{w},n}(\boldsymbol{a})-\frac1\pi\sum_{\ell=1}^{n-1} \sin\Biggl[\Biggl(\sum_{k=1}^{\ell}w_k\Biggr)\pi\Biggr] \int_{a_\ell}^{a_{\ell+1}} \prod_{k=1}^n|a_k-t|^{w_k} \frac{\textrm{d}\,t}{t}\le A_{\boldsymbol{w},n}(\boldsymbol{a}). \end{equation} Setting $n=2$ in \eqref{AG-New-eq1-weighted-z=0} leads to \begin{equation}\label{AG-New-n=2-weighted-z=0}\tag{5} a_1^{w_1}a_2^{w_2}=w_1a_1+w_2a_2-\frac{\sin(w_1\pi)}\pi \int_{a_1}^{a_2} \biggl(1-\frac{a_1}{t}\biggr)^{w_1} \biggl(\frac{a_2}{t}-1\biggr)^{w_2} \textrm{d}\,t \le w_1a_1+w_2a_2 \end{equation} for $w_1,w_2>0$ such that $w_1+w_2=1$.
There have existed more closely related conclusions published in the following references below.
References
Noticing that $(x-a)(b-x)=\left(\frac{b-a}{2}\right)^2-\left(x-\frac{a+b}{2}\right)^2$, we let $x-\frac{a+b}{2}=\frac{b-a}{2} \sin \theta$ and transforms the integral into $$ \begin{aligned}I&=\left(\frac{b-a}{2}\right)^2 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{\cos ^2 \theta}{\frac{b-a}{2} \sin \theta+\frac{a+b}{2}} d \theta \\ &=h^2 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{\cos ^2 \theta}{h \sin \theta+k} d \theta\end{aligned} $$ where $h=\frac{b-a}{2}$ and $k=\frac{a+b}{2}$.
$$ \begin{aligned} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{\cos ^2 \theta}{h \sin \theta+k} d \theta =& \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1-\sin ^2 \theta}{h \sin \theta+k} d \theta \\ =& \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left(-\frac{\sin \theta}{h}+\frac{k}{h^2}+\frac{1-\frac{k^2}{h^2}}{h \sin \theta+k}\right) d \theta\\ =& {\left[\frac{\cos \theta}{h}+\frac{k}{h^2} \theta\right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}+\frac{h^2-k^2}{h^2} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{d \theta}{h \sin \theta+k} } \quad (*)\\=& \frac{k \pi}{h^2}-\frac{k^2-h^2}{h^2} \cdot\frac{\pi}{\sqrt{k^2-h^2}}\\=&\frac{\pi}{h^2}\left(k-\sqrt{k^2-h^2}\right) \end{aligned} $$
We now conclude that
$$\boxed{ \int_a^b \frac{1}{x} \sqrt{(x-a)(b-x)} d x=\left(\frac{a+b}{2}-\sqrt{a b}\right) \pi}$$
Note:
Please refer to the post for (*).
