2

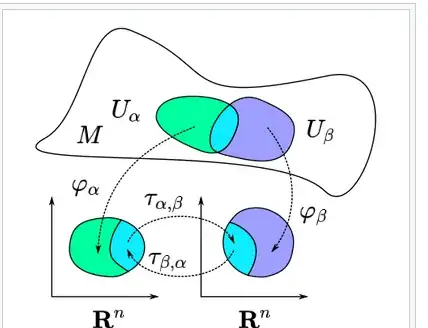
In my lectures notes, the definition of topological manifold is as follows:

A topological space $(X,\tau)$ that is connected, T2 and locally euclidean with a countable basis is called a topological manifold if $(A,\psi_1)$, $(B,\psi_2)$ are charts such that $A \cap B \neq \phi$ .

My question is about the countable basis,

1)is it referred to the locally euclidean space or to the whole $(X,\tau)$? I mean, are they talking about the basis of the domain of each chart, or about the whole space?

2) why should it be countable? Could you provide an example?

Please stick to topological manifolds, I've only seen this definition as the final part of a general topology course, I've seen some posts about, but they give examples that are too technical to understand, I would like a simple reason/example base on introductory general topology stuff

In particular, I would like to know if dropping the countability requirement affects the transition function $\tau_{\alpha, \beta}$ or the homeomorphisms $\varphi_\alpha$ ,$\varphi_\beta$ in the following scheeme? enter image description here

some_math_guy
  • 3,654
  • 1
    If I'm not wrong, countability is referred to the topological space $(X,\tau)$ (every chart, since it belongs to $\mathbb{R}^n$ has a countable basis). This property is not universially required though: it ensures the existence of the so called "partitions of unity", which are a fundamental tool for the development of the theory (but many authors drop this assumption) – qwertyguy Feb 15 '20 at 11:15
  • Not sure whether these answers satisfy you, but see here for some reasons: https://math.stackexchange.com/questions/2131530/why-is-important-for-a-manifold-to-have-countable-basis – Con Feb 15 '20 at 13:28
  • 1
    The simplest examples that aren't second-countable but satisfy the rest of the definition of "manifold" are the long ray and the long line; see https://en.wikipedia.org/wiki/Long_line_(topology) . If you like these (which I do), then you can all them manifolds by deleting the "countable basis" part of the definition of "manifold". If you'd rather never see such things again, then keep "countable basis" in the definition. – Andreas Blass Feb 15 '20 at 14:10

1 Answers1

4

The assumption means that $(X,\tau)$ has a countable base. It implies that $X$ has all sorts of nice properties (it will be paracompact, metrisable, $\sigma$-compact etc.) and will allow for so-called partitions of unity. Spaces like the long line are not second countable and lack the aforementioned properties. This older question and its answers go into more detail on why this matters in manifolds. Topologists do sometimes study general (not second countable , just locally Euclidean Hausdorff) manifolds and because of their nice local structure, if often turns out that even assuming something relatively weak (in general terms) on a manifold, means it will often have even nicer properties; this survey paper by Gauld gives some of these conditions. Your text basically wants to study metrisable manifolds, not the most abstract ones, like the Long line etc. This is common in more "geometric/differentiability" settings.

Henno Brandsma
  • 250,824
  • Does dropping the countability requirement affects the transition function $\tau_{\alpha, \beta}$ or the homeomorphisms $\varphi_\alpha$ ,$\varphi_\beta$ in the graphic I just added? if so, how? – some_math_guy Feb 15 '20 at 16:48
  • @juancarlosvegaoliver no, you can just use fewer of the sets. – Henno Brandsma Feb 15 '20 at 16:56