Yes. Variables are just place holders.
Congratulations! You just discovered trigonometry!
Think of what this means. If $(x,y)$ is a point on a circle with radius $r$ then $x^2 + y^2 = r^2$ which means there is always a right triangle that has has $|x|, |y|$ as sides and $r$ as a hypothesis.
In other words. If you take the point $A=(x,y)$; drop it to the $x$-axis and take the point $B= (x,0)$ and and $C = (0,0)$ then the triangle $\triangle ABC$ will always be a right triangle with a hypotenuse of length $r$.
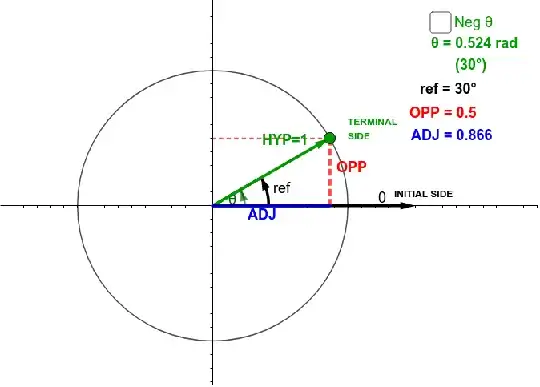
(image from here which discusses this very issue.)
Welcome to the wonderful world of trigonometry! (Seriously... Trigonometry is ENTIRELY about this.)
=====
Actually, all this is backwards.
FIRST we know that $A=(x,y)$ and $B=(x,0)$ and $C=(0,0)$ must be a right triangle becuase the $x$ and $y$ axis are perpendicular and $\overline {AB}$ is parallel to the $y$-axix.
And then BECAUSE it is a right triangle we know that $\overline {AC}$ which we know is equal to the radius of the circle, $r$ thatn $r^2 = (AC)^2= (AB)^2 + (BC)^2= x^2 + y^2$.
And that is how we came up with the formula for the circle in the first place!
Similarly, this is also how we came up with the distance formula. The distance between $(x_1, y_1)$ and $(x_2, y_2)$ is $\sqrt{(x_2-x_1)^2 + (y_2 - y_2)^2}$ because the points $(x_1, y_1), (x_2, y_1),(x_2, y_2)$ make a right triangle with sides of lengths $(x_2-x_1)$ and $(y_2 - y_2)$ and a hypotenuse the distance between the two points.
And a circle always having a distance of $r$ means for any $(x,y)$ on the circle that $r$, the distance between $(x,y)$ and $(0,0)$, must be $\sqrt{(x-0)^2 + (y-0)^2}$. Or in other words it must be that $x^2 + y^2 = r^2$.
