2

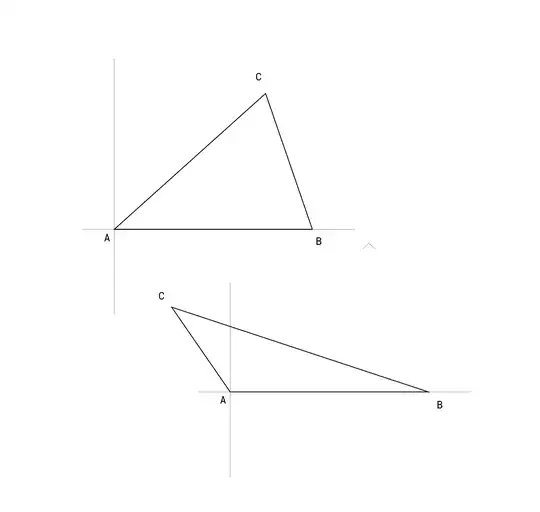
...such vertices (A,B,C):

  • A is the origin
  • B belongs to x axis
  • C is anywhere (or maybe C.y > 0) enter image description here

Why such a question ?

I'm looking for documentation in geometry, and a name could be an entry to begin.

NB: I'm trying to implement an algorithm to populate triangle faces of a mesh with random nodes (the blue pikes here). To generate the nodes it seems more convenient to work in 2D space. And to optimize computations it seems logic to convert the 3D triangle to a 2D triangle where the vertices are thus placed.

enter image description here

Shaun
  • 47,747
Joseph Merdrignac
  • 239
  • 3
    I don't think there is a widespread name for this setup, because with rotation and translation, you can place every triangle like this. – Botond Feb 05 '20 at 16:37
  • 1
    If there's a name for this configuration, I can't call it to mind at the moment. However, (and no doubt you know this, given the purpose of your inquiry) the matrix of coordinate vectors of the (non-origin) vertices is "(upper) triangular". (Likewise, for general simplex with a vertex at the origin, one on the $x$-axis, one on the $xy$-plane, one on $xyz$-space, etc.) Given that matrix decompositions into triangular matrices (eg, QR and LU) are a big deal, I imagine someone must have given a name to the corresponding arrangement of vertices. – Blue Feb 05 '20 at 19:31
  • @Botond yep, right, i was wondering if there is a name for a such a configuration as there is a name for the "unit circle". In 3D graphics triangles are everywhere and many things can be done in the local space of a triangle. So it may exists a name for that "small piece of space". – Joseph Merdrignac Feb 06 '20 at 21:17

3 Answers3

1

An angle drawn that way is in standard position. I couldn't find that phrase already being used for triangles, but if I were in your shoes, I might write something like "Analogous to angles in trigonometry, we say a triangle is in 'standard position' if...".

Mark S.
  • 25,893
  • Standard position is a good name, and failing to find a domain of maths corresponding to my research, i may use "Standard" in my code to distinguish such triangle from a regular random (3D) triangle. – Joseph Merdrignac Feb 06 '20 at 21:26
1

I see a connection of your issue with the representation of "the space of triangles" (initiated by Kendall) like in this rich reference. where triangular shapes have one horizontal side, WLOG because the shape is independent from its orientation Of course, it is the shape itself (like if your point $B$ is constraint to be fixed, say at $(0,1)$ ; the "size" dimension has to be added afterwards or more exactly in an independent manner.

Jean Marie
  • 88,997
0

No, I think it hasn't a special name. It's simply a triangle that can be isoschele, equilater, or rectangular and so on.

Matteo
  • 6,661