1

I'm interested in how the expected cosine proximity between a vector $x\in \mathbb{R}^N$ and a perturbed version of it, $\tilde{x}=x+\varepsilon$, where $x\sim \mathcal{N}(0,\sigma I_N)$ and $\varepsilon\sim \mathcal{N}(0,\tilde{\sigma}I_N)$, scales a a function of $N$.

(EDIT: Note that I should have written $\sigma^2, \tilde{\sigma}^2$, but as the answer below uses the above notation, I will keep this as is. So, for the following, $\sigma$ denotes the variance.)

That is, what is

$$ \mathbb{E}_{x,\varepsilon}[\cos(\theta)] = \mathbb{E}_{x,\varepsilon}\left[\left\langle \frac{x}{\| x\|} \cdot \frac{\tilde{x}}{\| \tilde{x}\|} \right \rangle \right] $$

as a function of $N$?

Without loss of generality, we can assume that $\sigma = \| x \| = 1$. We cannot assume that $\tilde{\sigma} \ll \sigma$, but - if it's helpful - we could assume that $\tilde{\sigma} \leq \sigma$.

I have tried writing out the integrals, but it's a mess, and I have the feeling that there should exist a much more elegant geometric solution, which eludes me at the moment.

If there is no immediate closed-form solution to the general problem, the situation where $N\gg 1$ is the most relevant for my specific application.

EDIT: Perhaps this could be useful: Expected value of dot product between a random unit vector in $\mathbb{R}^N$ and another given unit vector

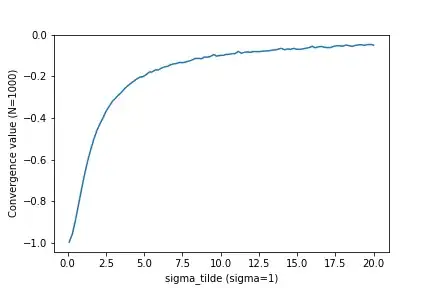
Another interesting aspect is how this expected value changes as a function of of the ratio between the two standard deviations. I have done some simulations on this:

For some ratio, the expected value always converges to some number for $N\rightarrow \infty$. In the plot below, the converged value (for $N=100$, which seemed to be more than enough) is plotted as a function of the ratio.

enter image description here

We clearly see that, as the size of the perturbation (captured by $\tilde{\sigma}$) increases, $x$ and $\tilde{x}$ become independent, and therefore orthogonal, which is expected.

Any insights would be appreciated!

Bobson Dugnutt
  • 10,912

1 Answers1

1

The expectation is undefined, as $\tilde x$ could be equal to $-x$. However, that event has measure zero so you can condition on it not being the case, or define the cosine to be zero in that case.

Let us assume $\|x\|=1$, as you did. No matter what vectors you sample, rotating them will not change the cosine and your distributions are invariant under orthogonal transformations, so you can assume $x=e_1=(1,0,0,\dots)$. Thus, using $\epsilon$ to denote the rotated vector in a slight abuse of notation, $$ \cos(\theta) = \frac{1+\epsilon_1}{\|\tilde x\|}. $$ So $$ \mathbb E[\cos(\theta)] = \mathbb E\left[\frac{1+\epsilon_1}{\|\tilde x\|}\right] $$

$$ = \frac{\mathbb E\left[1+\epsilon_1\right]}{\mathbb E\left[\|\tilde x\|\right]} - \mathbb E\left[(1+\epsilon_1)\left(\frac{1}{\|\tilde x\|}-\frac{1}{\mathbb E[\|\tilde x\|]}\right)\right] $$

$$ = \Theta\left(\frac{1}{(\sigma+\tilde\sigma)\sqrt{N}}\right) - \mathbb E\left[(1+\epsilon_1)\left(\frac{1}{\|\tilde x\|}-\frac{1}{\mathbb E[\|\tilde x\|]}\right)\right]. $$ I think it is clear that the r.h.s. of the difference vanishes with $N$.

For the second equality see

Koop, J. C. "On the derivation of expected value and variance of ratios without the use of infinite series expansions." Metrika 19.1 (1972): 156-170.

For the expected value of the norm see this.

cangrejo
  • 1,279
  • Thanks! By $\tilde{x}_1$, I'm assuming that you mean $e_1+\varepsilon$, and not the first element of $\tilde{x}$, right? Also, in the linked question regarding the expected value of the norm, which of the answers are correct? They are wildly different. I'm guessing you're using this result to say that the rhs. of the difference vanishes with $N$ - if not, what is your argument? It is not clear to me. – Bobson Dugnutt Jan 31 '20 at 09:20
  • @BobsonDugnutt Oh, that was just a typo I copy-pasted all over. It should be $\tilde x$. The result I'm using is that the expected norm is essentially $\sigma\sqrt N$ for $\mathcal N(0,\sigma I)$. – cangrejo Jan 31 '20 at 09:43
  • Wrt. the norm, I don't see the $\sqrt{N}$ anywhere in the answers to the linked question either. Also, shouldn't it be $1/\left(\sqrt{\sigma^2 + {\tilde{\sigma}}^2}\sqrt{N}\right)$, as the std. of the sum of two Gaussians is their std.s added in quadrature? – Bobson Dugnutt Jan 31 '20 at 11:52
  • @BobsonDugnutt That the expected value is a $\sigma\Theta (\sqrt N)$ is the last statement in the answer with 12 upvotes. The covariance matrix of a sum of independent multivariate Gaussian variables is the sum of the covariance matrices. Note that the diagonal of the covariance matrix is the variance of each variable, not the st. dev. – cangrejo Jan 31 '20 at 12:08
  • Ah, right, sorry, I miswrote in my question (I should have used $\sigma^2$ instead of $\sigma$), but I will leave it as is, as your question uses the same notation. Still, how do you see that the rhs. of the difference vanishes with $N$ (and with which rate)? – Bobson Dugnutt Jan 31 '20 at 12:20
  • @BobsonDugnutt If you expand the expression inside the expectation operator, the only term which might not be immediately clear is $\mathbb E[\epsilon_1/|\tilde x|]$. However, notice that $\epsilon_1$ does not grow with $N$, while $|\tilde x|$ does. I haven't analyzed it but my intuition is that it is also in the order of $1/((\sigma+\tilde \sigma)\sqrt N)$. – cangrejo Jan 31 '20 at 12:47
  • Okay, thanks. That is, however, the whole point of the question: To prove whether the difference vanishes (or becomes constant, which the simulation seems to suggest), so I'm leaving it open for now. – Bobson Dugnutt Feb 01 '20 at 10:59