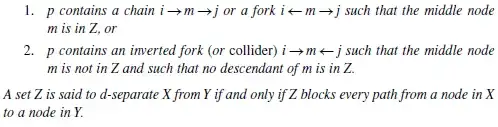2

In Pearl's Causality - Models, Reasoning and Inference (2009), he defines d-separation as follows:

enter image description here enter image description here

Let $X\perp\!\!\!\perp Y |Z$ mean "$Z$ d-separates $X$ from $Y$".

But there seems to be a weird edge case that satisfies this criterion, but actually shouldn't: We can have a situation where $X\subset Z$. E.g. imagine the case where $X=Z=\{V\}$, and $Y=\{W\}$.

Then we want that $X\perp\!\!\!\perp Y |Z$ holds, because we want $X\perp\!\!\!\perp Y |Z$ to coincide with the probabilistic notion of conditional independence, and clearly $X$ and $Y$ are conditionally independent given $X$. However, consider a simple graph consisting of nodes $\{V,W\}$, with an edge $V\to W$. Here, the path between $V$ and $W$ is not blocked, $X$ and $Y$ are not d-separated.

What am I missing here?

user56834
  • 12,323
  • Can you please add a causal diagram to illustrate your question? To me, with only two "vertices", it's not clear how you could have $d$-separation in the first place, since $d$-separation requires the existence of a chain, fork, or collider. All of those require three vertices. – Adrian Keister Feb 11 '20 at 18:27

1 Answers1

1

When at least one of the two nodes is fixed by the set of conditions, then it is trivial that the two nodes shall be conditionally independent, whatever other conditions ($C$) may apply, by the definition of conditional probability.

$$\begin{align}\mathsf P(X{=}x, Y{=}y\mid X{=}x, C)~&=~\mathsf P(X{=}x\mid X{=}x, C)\,\mathsf P(Y{=}y\mid X{=}x, X{=}x, C)\\[1ex]&=~\mathsf P(X{=}x\mid X{=}x, C)\,\mathsf P(Y{=}y\mid X{=}x, C)\end{align}$$

But neither of those end nodes is a chain, fork, or collider on any path between them, so they do not meet any of the criteria to cause d-separation of any path.

If there are no other nodes on the net d-seperates those two nodes, then they will not be d-separated.

That is okay, because d-separation on a DAG does not coincide with conditional independence.

d-separation is sufficient but not necessary for conditional independence between two nodes.

Graham Kemp
  • 133,231