I have an expression below which I need to do the laplace transform
Any help is highly appreicated.
The expression is :
$$ \frac{\exp\left(\frac{x}{2}\sqrt{(U/D)^2+4s/D}\right)}{s\sqrt{(U/D)^2+4s/D}} $$
The integral of Ron Gordon's expression:
The first expression on the solution was extracted from Wolfram from the following link:
http://bit.ly/YFbLfH
I will reduce this to an integral over the real line. Consider the integral in the complex plane:
$$\displaystyle \oint_C \frac{dz}{z} \frac{\exp{\left[\frac{x}{2} \sqrt{\left(\frac{U}{D} \right)^2 + 4 \frac{z}{D}}\right]}}{\sqrt{\left(\frac{U}{D} \right)^2 + 4 \frac{z}{D}}} e^{t z}$$
where $C$ is the following contour
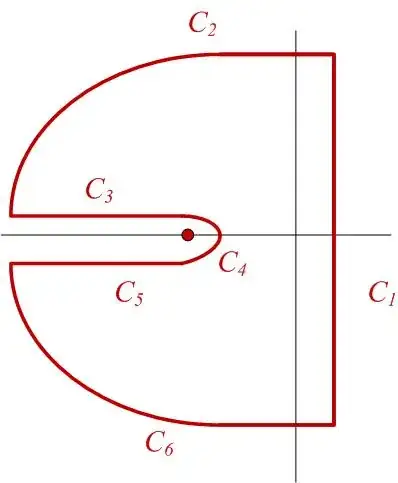
Note the point is the branch point. I will assert without proof that the integral vanishes along the sections $C_2$, $C_4$, and $C_6$ of $C$. This leaves $C_1$ (the ILT), $C_3$, and $C_5$. There is a pole within the contour at $z=0$, so by the residue theorem, we have
$$\frac{1}{i 2 \pi}\left [\int_{C_1} + \int_{C_3} + \int_{C_5} \right ]\frac{dz}{z} \frac{\exp{\left[\frac{x}{2} \sqrt{\left(\frac{U}{D} \right)^2 + 4 \frac{z}{D}}\right]}}{\sqrt{\left(\frac{U}{D} \right)^2 + 4 \frac{z}{D}}} e^{t z} = \frac{D}{U} e^{U x/(2 D)}$$
Along $C_3$, note that there is a branch point at $z=-U^2/(4 D)$. Thus we parametrize $z=-U^2/(4 D) + e^{i \pi} y$; the integral over $C_3$ becomes
$$-i \int_{\infty}^0 \frac{dy}{y+\frac{U^2}{4 D}} \frac{e^{i (x/2) \sqrt{y}}}{\sqrt{y}} e^{-t y}$$
Similarly, along $C_5$, let $z=-U^2/(4 D) + e^{-i \pi} y$; the integral over $C_5$ becomes
$$i \int_0^{\infty} \frac{dy}{y+\frac{U^2}{4 D}} \frac{e^{-i (x/2) \sqrt{y}}}{\sqrt{y}} e^{-t y}$$
Putting this all together as above, we get an expression for the ILT:
$$\frac{1}{i 2 \pi}\int_{c-i \infty}^{c+i \infty} \frac{ds}{s} \frac{\exp{\left[\frac{x}{2} \sqrt{\left(\frac{U}{D} \right)^2 + 4 \frac{s}{D}}\right]}}{\sqrt{\left(\frac{U}{D} \right)^2 + 4 \frac{s}{D}}} e^{t s} = \\ \frac{D}{U} e^{U x/(2 D)} - \frac{1}{\pi} \int_0^{\infty} \frac{dy}{y+\frac{U^2}{4 D}} \frac{\cos{[(x/2) \sqrt{y}]}}{\sqrt{y}} e^{-t y}$$
So evaluation of the posted ILT depends on the ability to evaluate
$$\int_0^{\infty} \frac{dy}{y+\frac{U^2}{4 D}} \frac{\cos{[(x/2) \sqrt{y}]}}{\sqrt{y}} e^{-t y}$$
This integral may be evaluated first by substituting $y=u^2$ and then applying the convolution theorem (or Parseval's theorem, depending on your mood). The substitution produces
$$\int_{-\infty}^{\infty} \frac{du}{u^2+b^2} e^{-a u^2} e^{i k u}$$
where $a = t$, $b^2=U^2/(4 D)$, and $k=x/2$. You may then use the convolution theorem on the Fourier transforms of the functions
$$\int_{-\infty}^{\infty} e^{-a u^2} e^{i k u} = \sqrt{\frac{\pi}{a}} e^{-k^2/(4 a)}$$
$$\int_{-\infty}^{\infty} \frac{du}{u^2+b^2} e^{i k u} = \frac{\pi}{b} e^{-b |k|}$$
Then
$$\int_{-\infty}^{\infty} \frac{du}{u^2+b^2} e^{-a u^2} e^{i k u} = \frac{1}{2 \pi} \sqrt{\frac{\pi}{a}} \frac{\pi}{b} \int_{-\infty}^{\infty} dk' e^{-(k-k')^2/(4 a)} e^{-b |k'|}$$
Frankly, the evaluation of this integral is straightforward but a mess, the derivation of which is not very instructive and will only serve to obfuscate the result. I leave it to the reader with assurances that I have done this out myself, by hand. The result is that
$$\int_0^{\infty} \frac{dy}{y+\frac{U^2}{4 D}} \frac{\cos{[(x/2) \sqrt{y}]}}{\sqrt{y}} e^{-t y} = \pi \frac{\sqrt{4 D}}{U} e^{U^2 t/(4 D)} \left [ e^{-U x/(4\sqrt{D})} \text{erfc}\left(-U \sqrt{\frac{t}{D}}+\frac{x}{4 \sqrt{t}}\right) + e^{U x/(4 \sqrt{D})} \text{erfc}\left(-U \sqrt{\frac{t}{D}}-\frac{x}{4 \sqrt{t}}\right) \right]$$
where erfc is the complementary error function. Plug this expression in the equation for the ILT and you are done.
