There's something strange about $\sum \frac 1 {\sin(n)}$.

Question

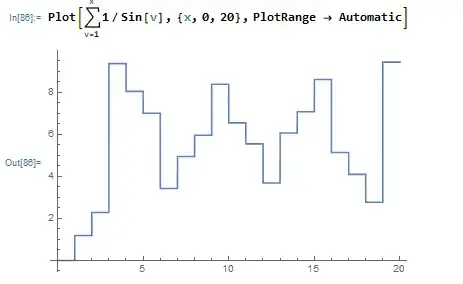
Clearly, $$\sum_{n=1}^\infty \frac 1{\sin(n)}$$ Does not converge (rational approximations for $\pi$ and whatnot.) For fun, I plotted $$P(x)=\sum_{n=1}^x \frac 1{\sin(n)}$$ For $x$ on various intervals. At first, I saw what you might expect:

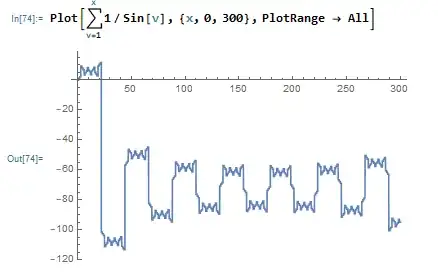
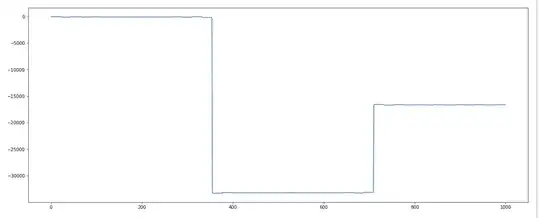
Which is $P(x)$ for $x \in [0,20]$ and then $[0,300]$. Seems a little self-similar, but whatever. Then I looked at $P(x)$ on the interval $[360,700]$:

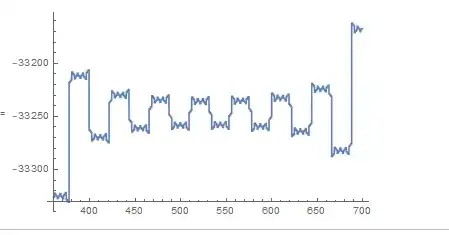
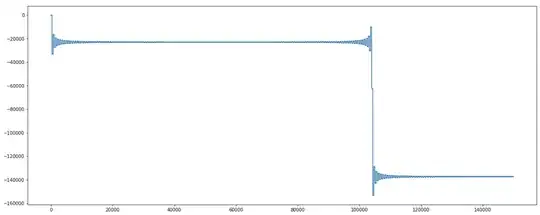
OK, that looks suspiciously like $P(x)$ on the interval $[0,300]$, but I'll toss out this coincidence as 'probably has to do with $\pi$ being irrational.' Here is $P(x)$ on $[700,1050]$:

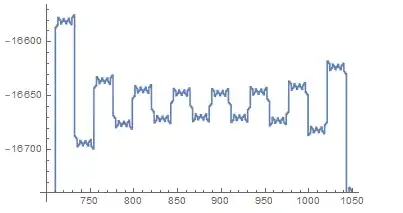
And I observe similar behavior on similar intervals.

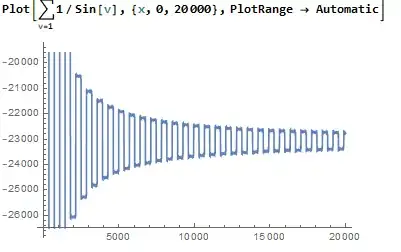
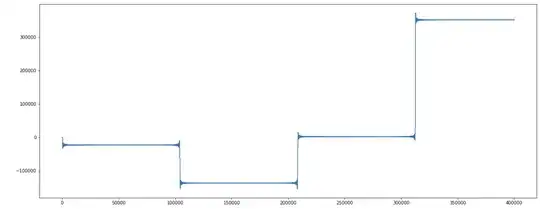
Putting it all together, here is $P(x)$ on $[0,20000]$:

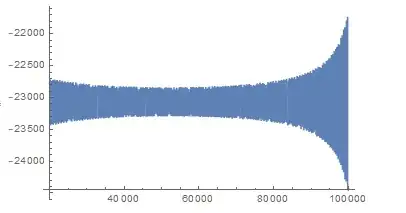
It's converging? Not quite. Here is $P(x)$ on $[20000,100000]$:

So again, we're seeing the function 'get closer and closer, then get farther and farther, all while alternating' from some value, just as we saw on the smaller intervals. I suspect that if my computer could handle $P(x)$ on $[100000,200000]$, we would see the same thing (on a larger scale), though I'm not sure.

So: what's going on here? How can we explain this fractal-ish behavior?

Edit: I wonder if $P:\mathbb{N} \to \mathbb{R}$ is injective...

Answer 1

The comments are well illustrating what's going on here. I'm writing the post to insert images and add a little explanation on continued fraction approximation.

As I mentioned above at comment, the 'best' rational approximations of irrational number come from its continued fraction. The first rational approximations of $\pi$ are $$3, \frac{22}{7}, \frac{333}{106}, \frac{355}{113}, \frac{103993}{33102}, \frac{104348}{33215}, \frac{208341}{66317}, \frac{312689}{99532}, \cdots .$$ (Mathematica code is like Table[FromContinuedFraction[ContinuedFraction[Pi, k]], {k, 1, 20}])

Recall the fact that, For an irrational number $x$ and its $n$th convergent $a_n/b_n$ (where $a_n$ and $b_n$ are coprime integers), we have $\left| x- \frac{a_n}{b_n}\right|<\frac{1}{b_n b_{n+1}}$ (**).

At a good approximation of $\pi$, say $355/113$, we have $355 \approx 113 \pi$ so $\sin (355) \approx 0$. Further, note that $\left|\pi - \frac{355}{113}\right|< \frac{1}{113\cdot 33102}$ by the above fact (**), so the difference is estimated as \begin{align*}|\sin(355)|& = |\sin(355 - 113\pi)|= \sin \left( 113\cdot \left|\pi-\frac{355}{113}\right|\right) & \\ & < \sin \frac{1}{33102} < \frac{1}{33102}\end{align*} so $\left|\frac{1}{\sin(355)}\right|>33102$, and thus the jump at $355$ is bigger than $30000$. (Numerical calculation gives $\frac{1}{\sin(355)}= -33173.708\dots$.)

(You see a jump at $710$, which is $355\times 2$. Note that $\pi \approx 355/113 = 710/226$)

You have the next continued fraction estimation $103993/33102$, i.e so there is a jump at $103993$. The size of this jump is similarly estimated as $>33215$.

Then the next jump is quite close since the next continued fraction estimation is $104348/33215$, with jump greater than $66317$.

This pattern, big jumps at numerator of continued fraction estimation of $\pi$ continues as follows.

If you are interested in python3 code:

import numpy as np 
from matplotlib import pyplot as plt
reciprocal_sin_sum = [0] 
for n in range(1, 400000):
    reciprocal_sin_sum.append(reciprocal_sin_sum[-1] + 1/(np.math.sin(n)))
plt.figure(figsize=(20,8))
plt.plot(range(len(reciprocal_sin_sum)), reciprocal_sin_sum)
plt.show()

Answer 2

Just for fun we could construct an integral representation of the sum: The inverse Mellin transform of $1/\sin(n)$ is $$ \mathcal{M}^{-1}\left[\frac{1}{\sin(n)}\right](x) = \frac{1}{1+x^\pi} $$ which perhaps shows the relationship to $\pi$ more clearly. Then we can formally write $$ \int_0^\infty \left(\sum_{k=0}^n x^k \right)\frac{1}{1+x^\pi} \; dx = \sum_{n=1}^{n+1} \frac{1}{\sin(n)} $$ or $$ \int_0^\infty \frac{(x^{n+1}-1)}{(x-1)(1+x^\pi)} \; dx = \sum_{n=1}^{n+1} \frac{1}{\sin(n)} $$ which apparently works for integer $n$. Now we can also numerically interpolate for some fractional $n$ such as $n=1/2$, although I can't vouch for the correctness of this continuation... This leads to a guess of the infinite limit of $$ \int_0^\infty \frac{1}{(1-x)(1+x^\pi)} \; dx = \sum_{n=1}^{\infty} \frac{1}{\sin(n)} \approx 1.256628 $$ although I'm not sure if the numeric integration just spat out some nonsense there... The residue at $x=1$ appears to be $-1/2$.