1

I am trying to make a geodesic dome 2v in Solidwork just for fun.

I use this dome calculator : http://www.domerama.com/calculators/2v-geodesic-dome-calculator/

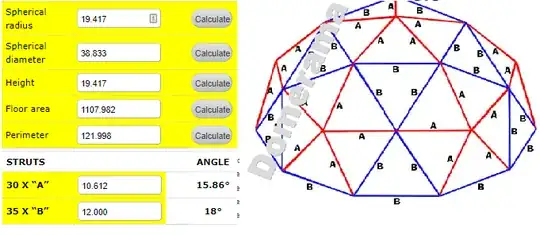
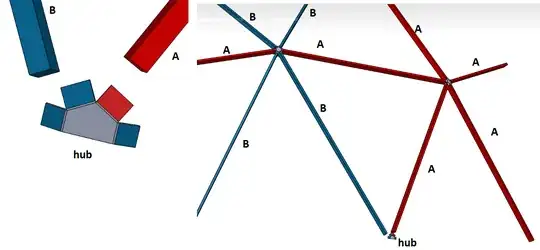
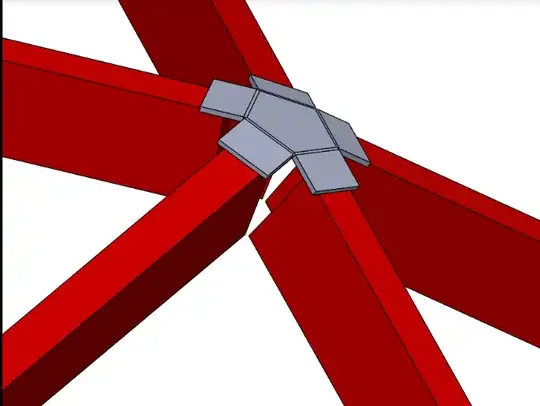
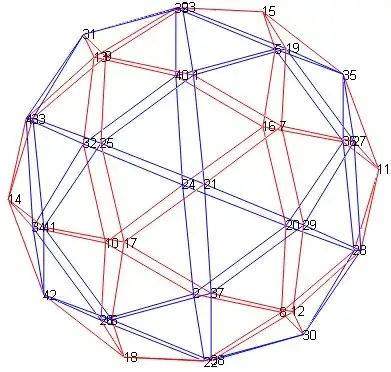
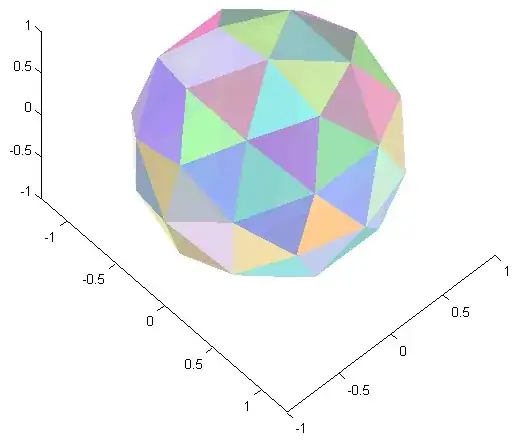
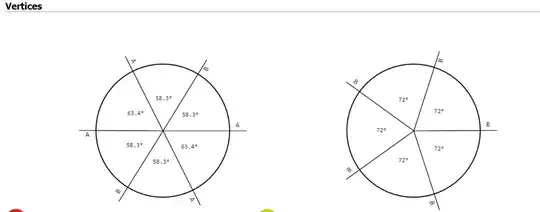
enter image description here

The problem is once I start the assembly, the first joint doesn't allign properly.

Is the calculator right ? I tried other calculators and they gave me the same results. What am I doing wrong ?

Here is the assembly made with sheet metal bending & 2x4 wood in solidwork:

So the red bend is at 15.86 degrees and the blue bend is at 18 degrees

enter image description here

See the little hub at the bottom right of the picture ? It should fit perfectly with the B and A strut!

Here is the 6 ways hub :

enter image description here

Here is the 5 ways hub:

enter image description here

Take note that all the strut are at the same distance into the hub so the ratio is respected.

What is wrong with my method ?

Christophe Chenel
  • 111
  • Please, could you explicitate what you mean when you say "the first joint doesn't align properly." ? 1) Which joint are you thinking to and 2) "doesn't align with what" ? – Jean Marie Jan 18 '20 at 19:49
  • A link among many others, with original answers : https://stackoverflow.com/questions/3031875/math-for-a-geodesic-sphere/3033370#3033370 – Jean Marie Jan 18 '20 at 21:13
  • The strut A and B shiuld fit properly into the hub socket. See bottom right of the second picture. – Christophe Chenel Jan 18 '20 at 21:25

2 Answers2

1

In fact the dihedral angles should be (in decimal degrees) :

$$18.03° \ \ \ \text{and} \ \ \ 22.46°$$

I find back your first angle but the second one is indeed in disagreement with your $15.86°$...

How did I obtain this result ?

This geodesic dome is a half of a volume called Pentakis icosidodecahedron

enter image description here

that I have been able to "construct" using the rich data found in http://dmccooey.com/polyhedra/PentakisIcosidodecahedron.txt but with a treacherous aspect, the points are not on a same sphere ! It took me some time before understanding and correcting it...

The following Matlab program that has allowed me to draw the figure and obtain the angles (think to scroll it) uses classical formulas with cross product and dot product :

  • The normal to triangular face $ABC$ is given by $\vec{n}=\vec{AB} \times \vec{AC}.$

  • The angle $a$ between two (normalized) normals is such that $\cos(a)=\vec{n_1}.\vec{n_2}.$

%Pentakis Icosidodecahedron 
% http://dmccooey.com/polyhedra/PentakisIcosidodecahedron.txt
clear all;close all;hold on;axis equal;
C0 = sqrt(5 * (5 - 2 * sqrt(5))) / 5
C1 = sqrt(10 * (5 - sqrt(5))) / 10
C2 = (6 * sqrt(5) + sqrt(2 * (85 - sqrt(5))) - 16) / 19
C3 = sqrt(10 * (5 + sqrt(5))) / 10
C4 = (7 - 5 * sqrt(5) + sqrt(2 * (125 + 41 * sqrt(5)))) / 19
C5 = sqrt(10 * (5 - sqrt(5))) / 5
T=...
[[0.0, 0.0,  C5];[0.0, 0.0, -C5];[ C5, 0.0, 0.0]
[-C5, 0.0, 0.0];[0.0,  C5, 0.0];[0.0, -C5, 0.0]
[ C2, 0.0,  C4];[ C2, 0.0, -C4];[-C2, 0.0,  C4]
[-C2, 0.0, -C4];[ C4,  C2, 0.0];[ C4, -C2, 0.0]
[-C4,  C2, 0.0];[-C4, -C2, 0.0];[0.0,  C4,  C2]
[0.0,  C4, -C2];[0.0, -C4,  C2];[0.0, -C4, -C2]
[ C0,  C1,  C3];[ C0,  C1, -C3];[ C0, -C1,  C3]
[ C0, -C1, -C3];[-C0,  C1,  C3];[-C0,  C1, -C3]
[-C0, -C1,  C3];[-C0, -C1, -C3];[ C3,  C0,  C1]
[ C3,  C0, -C1];[ C3, -C0,  C1];[ C3, -C0, -C1]
[-C3,  C0,  C1];[-C3,  C0, -C1];[-C3, -C0,  C1]
[-C3, -C0, -C1];[ C1,  C3,  C0];[ C1,  C3, -C0]
[ C1, -C3,  C0];[ C1, -C3, -C0];[-C1,  C3,  C0]
[-C1,  C3, -C0];[-C1, -C3,  C0];[-C1, -C3, -C0]];
for k=1:42
    T(k,:)=T(k,:)/norm(T(k,:));%all points are now on the (unit) sphere !
end;
n=@(p,q,r)(cross(T(q,:)-T(p,:),T(r,:)-T(p,:)));%normal to face (p,q,r)
for k=1:42
    text(T(k,1),T(k,2),T(k,3),num2str(k));
end;
n1=n(7,1,21);n1=n1/norm(n1);
n2=n(7,1,19);n2=n2/norm(n2);
n3=n(1,21,25);n3=n3/norm(n3);
a12=acos(n1*n2')*180/pi % angle at red junction
a13=acos(n1*n3')*180/pi % angle at blue junction
for p=1:42
    for q=p+1:42;
        no=norm(T(p,:)-T(q,:));%the two lengths are 0.618 and 0.5465
        if abs(no-0.618)<0.005 || abs(no-0.5465)<0.005
           c='r';
           if abs(n-0.618)<0.005; 
              c='b'
           end;
           I=[p,q];
           plot3(T(I,1),T(I,2),T(I,3),c);
        end;
    end;
end;
view([-4,0]);
figure(2);hold on;axis equal;
x=T(:,1);y=T(:,2);z=T(:,3);
K=convhull(x,y,z); % convex hull
for k=1:80
   I=K(k,:);colo=0.5+0.5*rand(1,3);
   fill3(T(I,1),T(I,2),T(I,3),colo,'edgecolor','none');alpha(0.9)
end;

enter image description here

Remark : one of the lengths is equal to $\Phi -1$ ($\Phi$ = Golden Ratio)

Community
  • 1
Jean Marie
  • 88,997
  • I understand that the formula for finding the side length of the equilateral triangles is your radius multiplied by Phi - 1, but how is the 0.5465 value calculated for determining the equal sides to the isosceles triangle? – mkinson Sep 18 '20 at 12:41
  • if abs(no-0.618)<0.005 || abs(no-0.5465)<0.005 – mkinson Sep 19 '20 at 20:38
  • @mkinson I have an answer: it is $\sqrt{(C_3-1)^2+C_1^2} \approx 0.5465$ i.e. the distance between vertices $(0,1,0)$ and $(0,C_3,C_1)$ (among others vertices, I have looked for the simplest ones). I have attempted to simplify a little the expression above in order to express it as a function of $\Phi$ but with no avail... – Jean Marie Sep 20 '20 at 09:05
  • Thank you Jean Marie, on another site I found that a simplistic method of finding the side lengths of the triangles in a geodesic dome require multiplying the radius by phi-1 for the equilateral triangles, and that 0.5465 value by the radius for the isosceles triangles with phi-1 * r for the base. Never understood where that value came from. – mkinson Sep 21 '20 at 17:15
  • @mkinson Very interesting. I will attempt to make the connection with the rather complicated value I gave you. – Jean Marie Sep 21 '20 at 17:39
  • 1
    @mkinson I have simplified the expression I gave you; I obtain : $\sqrt{2-2\sqrt{\frac{\Phi}{\sqrt{5}}}} \approx 0.546533057825343...$ – Jean Marie Sep 22 '20 at 07:20
  • Thank you @Jean Marie! That is exactly what I was trying to find. – mkinson Sep 22 '20 at 11:08
  • You can simplify that number further eliminating Phi entirely with sqrt(2 - sqrt(2 + 2/sqrt(5))) – mkinson Sep 22 '20 at 11:21
  • @mkinson Right! May I ask you why you are interested into geodesic domes ? On my side, I had noticed them before trying to answer to the question of the OP as a cousin structure of the zonotopes: see https://math.stackexchange.com/q/2127476. – Jean Marie Sep 22 '20 at 11:50
  • I am considering designing a geodesic home. I saw a bunch of fantastic design ideas, one including dozens of preformed triangle frames roughly 81.9 cm along the base. – mkinson Sep 22 '20 at 14:04
0

The problem was the hub!

The construction of the hub must be made out from any hexagon... each Vertice/Hub has angle in its construction. I finally found a calculator that gives the information for the hub:

enter image description here

http://acidome.ru/lab/calc/#1/1_Piped_D200_2V_R6_beams_150x50

Christophe Chenel
  • 111