-1

I don't understand how there is an uncountable infinite amount of real numbers. Why can't we do the same thing with fractions (there is a countable amount of fractions). We do this by creating a table where the horizontal axis lists all the numbers from 0 too infinity. The vertical axes lists all the powers of ten from 0 too -infinity. If we would fill the table we would have all real numbers. We can make a list of this by drawing a line criss-cross through the table. This table can be viewed by clicking the link.

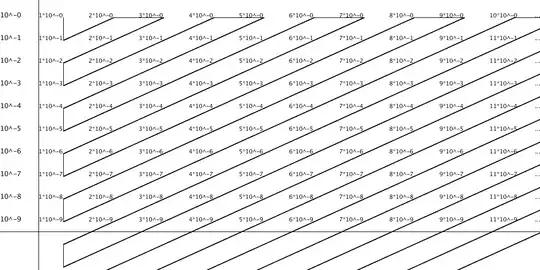
*How such a set should be ordered*

Could somebody please explain what is wrong with my thinking. Thank you.

Cabbelbeb C
  • 1

1 Answers1

5

Your method isn't even counting all rational numbers. For instance, the number $\frac13=0.\overline3$ doesn't occur in the table because there is no such natural number as $\overline3$ with an infinite number of digits.

  • I don't understand that. Natural numbers are all the numbers from 0 too infinity. Why wouldn't a number with an infinite amount of threes be part of that. Wouldn't that be infinity? – Cabbelbeb C Jan 06 '20 at 21:25
  • @CabbelbebC "Natural numbers are all the numbers from 0 too infinity." Not inclusively, though. Intuitively, the natural numbers are the things you can reach by applying "$+1$" to $0$ finitely many times. (This is only intuitive since "finite" needs to be defined; the formal approach to $\mathbb{N}$ is a bit more complicated.) So no, an expression like "$11111....$" or "$...11111$" is not a natural number. – Noah Schweber Jan 13 '20 at 17:13
  • It may help to think about induction, which is really the defining property of $\mathbb{N}$. Intuitively, we want to look at the property "has only finitely many digits" (again, ignoring the issues with the word "finite" for now). Clearly $0$ has only finitely many digits, and if $n$ has only finitely many digits then so does $n+1$, so by induction all natural numbers have only finitely many digits. Of course this isn't really rigorous, but it should help motivate the idea of $\mathbb{N}$ being "relatively small." – Noah Schweber Jan 13 '20 at 17:15