2

I have been having some problems with exercise 1.4.A in Vakil's Foundation of Algebraic Geometry. I feel like it's really basic (it's marked as a "reality check") and yet I can't seem to solve it.

1.4.A. Suppose that the partially ordered set $\mathcal{J}$ has an initial object $e$. Show that the limit of any diagram indexed by $\mathcal{J}$ exists.

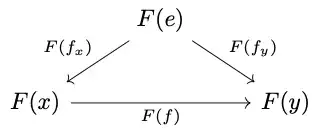
Proof attempt. Since $e$ is initial in $\mathcal{J}$, for every $x \neq e$ of $\mathcal{J}$ there is a unique arrow $f_x : e \to x$. Given a diagram $F : \mathcal{J} \to \mathcal{C}$, my idea was to have its limit be $F(e)$ along with all the arrows $F(f_x)$. First we prove that it is a cone: if $f : x \to y$ is any arrow in $\mathcal{J}$ then the triangle

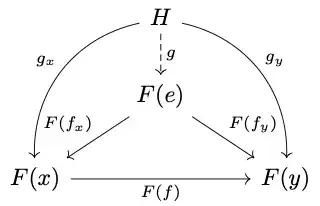
enter image description here

commutes because $$ F(f) \circ F(f_x) = F(f \circ f_x) = F(f_y), $$ where the last equality follows from the fact that $f \circ f_x$ and $f_y$ are both arrows $e \to y$ and are thus equal (equality can come either from $\mathcal{J}$ being a poset or from $e$ being initial). Hence this is a cone. To be a limit, it needs to satisfy the following universal property: given any object $H$ in $\mathcal{C}$ and arrows $g_x : H \to F(x)$ and $g_y : H \to F(y)$ with $F(f) \circ g_x = g_y$, there exists a unique arrow $g : H \to F(e)$ through which $g_x$ and $g_y$ factor, i.e. this diagram

enter image description here

commutes.

Here is where I get stuck. I can't find any "obvious" maps $H \to F(e)$, let alone any that make the diagram commute. I can't even make use of the fact that $e$ is initial, since the arrow goes in the wrong direction (it wouldn't matter anyway, since $H$ need not be in the image of $F$). Moreover, I haven't used the fact that $\mathcal{J}$ is a poset, since the commutativity of the first diagram could have just been proven using the fact that $e$ is initial.

So, my questions are:

  1. Am I right in thinking that the limit is $F(e)$ (with the unique maps)?

  2. If so, how can I prove the existence of $g$? What am I missing?

  3. Does the poset structure matter or could the hypothesis be broadened to small categories $\mathcal{J}$ with an initial object?

I'm almost sure I am missing something tremendously trivial, so a super small hint should be fine. Thank you in advance for your help.

Arnaud D.
  • 21,484
Lorenzo Riva
  • 389
  • 1
    Related : https://math.stackexchange.com/questions/1210440/given-a-mathcalc-rightarrow-mathcale-when-does-operatornamecolim – Arnaud D. May 22 '20 at 11:47

1 Answers1

3

There's a map $H\to F(e)$ given by assumption, namely $g_e$!

As to your other questions, yes, you have the correct limit; no, it does not matter that $\mathcal J$ is a poset.

Kevin Carlson
  • 54,515
  • Got it! Thank you, Kevin. I was looking at the problem one diagram at a time rather than as a whole. In fact, the way I stated the universal property is wrong: I should have written "... and an arrow $g_x : H \to F(x)$ for all objects $x$ of $\mathcal{J}$". – Lorenzo Riva Jan 02 '20 at 18:19
  • Is the poset condition required to show the uniqueness of the map g? – AXidenT May 26 '20 at 09:38
  • @AXidenT No, the same result is true for any category. – Kevin Carlson May 26 '20 at 15:53
  • Just out of curiosity or as an example, then by this result, can we conclude that pushforward kind of diagrams always have limit, or for example $\cdot\to\cdot\to \cdots\to $ has also limit which is the left-most dot. – Micheal Brain Hurts May 17 '23 at 19:46
  • @MichealBrainHurts I don’t know what “pushforward kind of diagrams” means but the specific diagram you showed has an initial object, and so yes, its limit is the value at the initial object. – Kevin Carlson May 17 '23 at 19:51