I tried to solve $\int_0^{+\infty} \frac{\ln{x}}{(x+1)(x^2+1)} dx$ by calculating the integral $\int_0^{+\infty} \frac{\ln^2{x}}{(x+1)(x^2+1)} dx$.
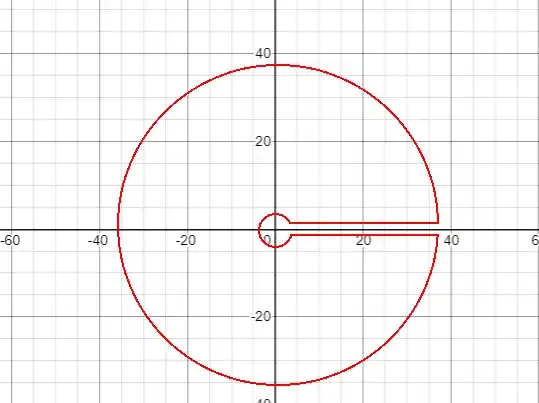
At first I precalculated the integral $\int_C \frac{\ln^2{z}}{(z+1)(z^2+1)} dx$, where $C$ is the contour like on the image:
So,
$$\int_C \frac{\ln^2{z}}{(z+1)(z^2+1)} dz = \int_{B(0,\epsilon)} \frac{\ln^2{z}}{(z+1)(z^2+1)} dx +$$ $$+ \int_{R_{up}^+} \frac{\ln^2{z}}{(z+1)(z^2+1)} dz + \int_{B(0,R)} \frac{\ln^2{z}}{(z+1)(z^2+1)} dz + \int_{R_{down}^+} \frac{\ln^2{z}}{(z+1)(z^2+1)} dz =$$ $$= 0 + \int_0^{+\infty} \frac{\ln^2{x}}{(x+1)(x^2+1)} dx + 0 + \int_{+\infty}^0 \frac{(\ln{x} + 2i\pi)^2}{(x+1)(x^2+1)} dx =$$ $$= - 4i\pi \int_0^{+\infty} \frac{\ln{x}}{(x+1)(x^2+1)} dx + 4\pi^2 \int_0^{+\infty} \frac{1}{(x+1)(x^2+1)} dx$$
But according to the Cauchy Residue Theorem,
$$\int_C \frac{\ln^2{z}}{(z+1)(z^2+1)} dz = 2i\pi (res_{z=-1} f(z) + res_{z=-i} f(z) + res_{z=i} f(z)) =$$ $$= 2i\pi \Big( \frac{\ln^2(-1)}{(-1)^2+1} + \frac{\ln^2(-i)}{(-i+1)(-i-i)} + \frac{\ln^2{i}}{(i+1)(i+i)} \Big) =$$ $$= 2i\pi \cdot \Big( -\frac{3\pi^2}{8} \Big) = -\frac{3i\pi^3}{4}$$
Since $\int_0^{+\infty} \frac{1}{(x+1)(x^2+1)} dx = \frac{\pi}{4}$, I can find the answer on my question:
$$\int_0^{+\infty} \frac{\ln{x}}{(x+1)(x^2+1)} dx = \frac{4\pi^2 \cdot \frac{\pi}{4} + \frac{3i\pi^3}{4}}{4i\pi} = \frac{\pi^2}{4i} + \frac{3\pi^2}{16} = - \frac{i\pi^2}{4} + \frac{3\pi^2}{16}$$
But I know that the correct answer is $- \frac{\pi^2}{16}$. It seems very strange that I have imaginary part left. I've tried to find solutions for the same integrals, but they just use keyhole contour as I do and it's okay. Can you help me to find a mistake?