0

I am currently reading Katok's Fuchsian Groups and I am trying to understand the proof the following theorem

$\textbf{Theorem 2.2.1.}$ $G$ acts properly and discontinuously on $X$ if and only if each point $x \in X$ has a neighborhood $V$ such that $$T(V) \cap V \neq \emptyset$$ for only finitely many $T \in G.$

$\textbf{Notes:}$

  1. $X$ is a metric space.

  2. $G$ is a group of isometries.

  3. There's a similar question here, but the following question is not the same as in the post mentioned. (Actually I asked a similar question a few hours ago, but it was a failure).

The proof goes as follows:

$G$ acts properly and discontinuously on $X.$ $\Rightarrow$ $Gx$ is discrete and $G_x$ is finite for each point $x.$ $\Rightarrow$ For any point $x$ exist a ball $B_\varepsilon (x)$ containing no points of $Gx$ other than $x.$ Now consider $V \subset B_{\varepsilon /2}.$ $\Rightarrow$ $T(V) \cap V \neq \emptyset$ implies that $T \in G_x.$

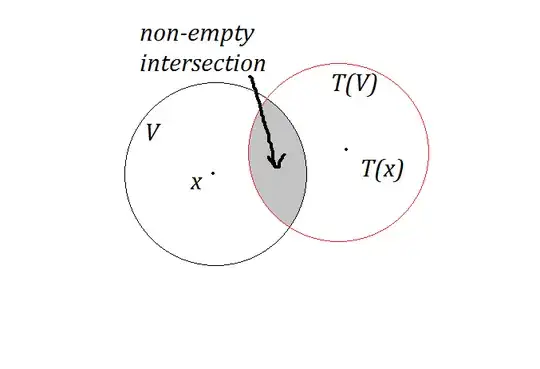
Why this last assertion is true? It may occur this:

enter image description here

In the picture, it is clear that $T(V) \cap V \neq \emptyset,$ but $T \notin G_x$ since $T(x) \neq x.$

It is clear that the intersection is non-empty even when that intersection doesn't contain elements of $G_x.$ Am I missing something? Thanks in advance. (PD: I have not taken Topology yet)

Community
  • 1
rowcol
  • 917

1 Answers1

1

Let's talk through it. The claim that $Gx$ is discrete and $G$ acts by isometries asserts that there is a positive minimum distance between distinct elements of $Gx$, i.e. that

$$\epsilon := \inf\{ d(x,y) : y \in Gx, y \neq x\} > 0.$$

So take $V= B_{\epsilon/2}(x)$. Suppose we have $T \in G$ with $T(V) \cap V \neq 0$. That is, there is some point $p \in T(V) \cap V$. Then both distances $d(p,x)$ and $d(p,Tx)$ are strictly smaller than $\frac \epsilon2$. The triangle inequality then implies $$d(x,Tx) \le d(p,x) + d(p,Tx) < \epsilon.$$

This implies $Tx = x$, i.e. that $T \in G_x$.

Robbie Lyman
  • 4,000