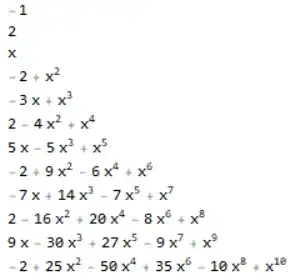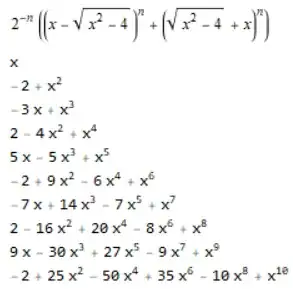4

The problem says :

Find all polynomials $P(x)$ with odd degree such that $$P(x^2 - 2) = P^2(x)-2$$

I tried a lot if ways (using high school mathematics) but the only solution I have so far is $P(x) = x$. Can anyone solve this problem using only high school mathematics ?

PS: I have reduced the solution set to the subset of all polynomials with leading coefficient 1.

N. F. Taussig
  • 79,074
Amanuel Getachew
  • 452

3 Answers3

2

This extended comment has the sole purpose of showing a simple Mathematica code to print the $P(x)$ polynomials up to the tenth degree that satisfy the relation $P(x^2-2) - (P(x))^2 + 2 = 0$.

P[x_] = Sum[ToExpression[StringJoin["a", ToString[n]]] x^n, {n, 0, 10}];
coeff = CoefficientList[P[x^2 - 2] - P[x]^2 + 2, x];
zeros = ConstantArray[0, Length[coeff]];
sol = Solve[coeff == zeros];
poly = Table[P[x] /. sol[[n]], {n, Length[sol]}];
TableForm[Sort[poly]]

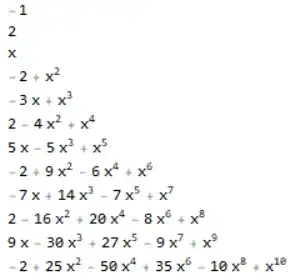
enter image description here

It's clear that, for $n \ge 1$, behind all this there is a sequence function, in fact:

Q[x_] = FindSequenceFunction[Sort[poly][[3 ;; All]], n];
TraditionalForm[Q[x]]
TableForm[Table[Expand[Q[x]], {n, 10}]]

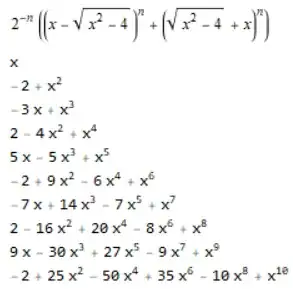
enter image description here

From this simple numerical experiment I deduce that the relation:

$$P(x^2-2) - (P(x))^2 + 2 = 0$$

is satisfied by:

$$ P(x) = -1 \; \; \; \vee \; \; \; P(x) = \left(\frac{x-\sqrt{x^2-4}}{2}\right)^n + \left(\frac{x+\sqrt{x^2-4}}{2}\right)^n $$

where is assumed $n \in \mathbb{Z}$.

  • 1
    Two observations. First, your results seem to satisfy the two-term recurrence relation $P_{n+1}(x)=xP_n(x)-P_{n-1}(x)$. I don't see any obvious reason why that should always be the case. Second, writing $P(x)=Q(x)+x$ leads to $Q(x^2-2)=Q(x)(Q(x)-2)$, which means that if $x_0$ is a root of $Q$ then so is $x_0^2-2$, which means $(x_0^2-2)^2-2$ is too, and so forth. This suggests it may be worth looking at how $P(x)-x$ factors for your $P$s. – Barry Cipra Dec 16 '19 at 01:22
  • Let $Q_n$ be the polynomial of degree $n>0$ such that $Q_n(x+x^{-1}) = x^n+x^{-n}$. Then $Q_n$ satisfies the requested relation. These are the non-constant polynomials listed here. – WimC Dec 16 '19 at 06:30
1

Let $K(x) = x^2-2$ and for any $n \geq 1$ let $K^n(x)$ be repeated application of $K$ (so $K^1(x)=K(x)$ and $K^{n+1}(x) = K(K^n(x))$). Then for fixed $x$ the sequence $K^n(x)$ is bounded if and only if $\lvert x \rvert \leq 2$. Since $P(K^n(x))=K^n(P(x))$ it follows that $\lvert P(x) \rvert \leq 2$ for all $\lvert x \rvert \leq 2$. As noted, the leading coefficient of $P$ is $1$.

It is well known that a polynomial $T$ of degree $n$ with leading coefficient $2^{n-1}$ maps $[-1,1]$ into $[-1,1]$ if and only if $T=T_n$ is a Chebyshev polynomial of the first kind.

Conclude that $P(2x)/2 = T_n$ where $\deg(P)=n$. So $P$ is characterized by $$P(x+x^{-1})=x^n+x^{-n}.$$ It is easy to check that such a polynomial indeed has the required property.

WimC
  • 33,414
  • 2
  • 52
  • 98
1

For every $n\ge 0$ there exists a unique polynomial of degree $n$ such that $$P_n(t+1/t) = t^n + 1/t^n$$ For instance, $P_0(x) = 2$, $P_1(x) =x$, $P_2(x) = x^2-2$, and so on. It is easy to see that $$P_m\circ P_n(x) = P_{mn}(x)$$ so any two $P_m$'s commute. In particular, $P_n(P_2(x))= P_2(P_n(x))$. Let now $n>0$ and $P$ of degree $n$. We can write $$P(x) = \alpha \cdot P_n(x) + Q(x)$$ where $\alpha \ne 0$, and $Q$ is of degree at most $n-1$. Assume that we have $$P(x^2-2) = P(x)^2-2$$ We get $$\alpha P_n(x^2 - 2) + Q(x^2 -2) = (\alpha P_n(x)+ Q(x))^2 - 2$$ or, since $P_n$ commutes with $x^2-2$ $$\alpha (P_n(x)^2 -2) + Q(x^2-2) = \alpha^2 P_n(x)^2+ 2 \alpha P_n(x) Q(x) + Q(x)^2 -2$$ The leading terms have to match, so $\alpha = 1$. We now get $$ Q(x^2 -2) = 2 P_n(x) Q(x) + Q(x)^2$$ If $Q\ne 0$ then LHS has degree less than RHS, contradiction.

Therefore, for any $n>0$ the only polynomial of degree $n$ commuting with $x^2-2$ is $P_n(x)$. Note that there are two constant polynomials that commute, $2$ and $-1$.

orangeskid
  • 56,630