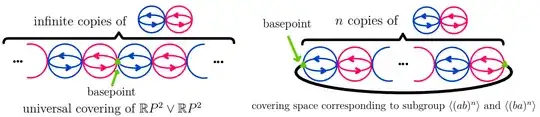
In the following pictures, green dots means basepoints, black curve means its two endpoints are attached. Covering map maps blue $S^2$ to $X_1$ and red $S^2$ to $X_2$.
Let $X_1$ and $X_2$ denote the first and second copy of $\mathbb RP^2$.
$\pi_1(X_1)=\mathbb Z_2=\langle a \rangle,\ \pi_1(X_2)=\mathbb Z_2=\langle b \rangle$.

$1$. For trivial subgroup $1$, it corresponds to the the universal cover, i.e. the infinite chain of $S^2$.
$2$. For subgroup isomorphic to infinite cyclic group $\mathbb Z$, it is generated by $(ab)^n$ or $(ba)^n$ of index $2n$ $(n \geqslant 1)$ and it corresponds to a "necklace" of $2n$ copies of $S^2$.
$3$. For subgroup isomorphic to $\mathbb Z_2$, it's generated by $(ab)^{m}\cdot a$ or $(ba)^{m}\cdot b$ $(k\geqslant 0)$ and it corresponds to $\mathbb RP^2$ attached to an infinite chain of $S^2$.
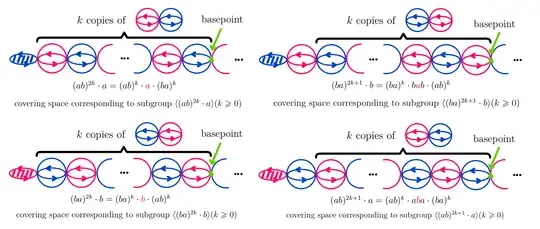
$4$. For subgroup isomorphic to the infinite dihedral group $\mathbb Z_2 * \mathbb Z_2$, it's generated by $(ab)^n$ and $(ab)^m \cdot a$ $(m\leqslant n)$ and it corresponds to a finite chain of $S^2$'s with both ends attached an $\mathbb RP^2$.




