3

Let $M$ be a smooth manifold. Let $C \subseteq M$ be a simply connected closed set. Is it always possible to find a simply connected open set $U \subseteq M$ such that $C \subseteq U$?

Math_tourist
  • 439

1 Answers1

4

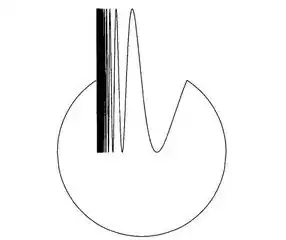
No. Consider $M=\mathbb{R}^2\backslash\{0\}$ and let $C$ be the topologist's sine circle:

enter image description here

around the origin $0$. It is simply-connected. Since you cannot cross from the right side to the left side via upper half. And so the image of any path is contained in an arc.

The point is that any open neighbourhood of that space contains $S^1$ (up to deformation anyway) which cannot be contracted due to $0$ not belonging to $M$.

freakish
  • 47,446
  • Thanks for the answer Nice example! I believe that the key point here is that the inclusion map $\iota \colon C \to M$ is not a proper function in your case. If I assume properness, do you think the answer is "yes"? – Math_tourist Nov 22 '19 at 13:31
  • @Math_tourist "proper" as in "inverse image of compact is compact"? Note that $C$ is compact (closed and bounded in $\mathbb{R}^2$) and so any continuous map starting from $C$ is proper, including the inclusion map $C\to M$. – freakish Nov 22 '19 at 13:35
  • oh right!! Forgot what I said. So then what is the key property that makes the counterexample work? I mean, are there any reasonable assumptions one can put on $C$ in order to get the answer "yes" to my question? Like locally path connectedness or something? – Math_tourist Nov 22 '19 at 13:40
  • 1
    @Math_tourist locally path connected might work. In this situation I think you can generate a small open neighbourhood that deformation retracts onto $C$ (and so shares its homotopy type). But this is my intuition only, needs verifying. I encourage you to ask a separate question. – freakish Nov 22 '19 at 13:42
  • I asked this new question https://math.stackexchange.com/questions/3446579/simply-connected-neighbourhood-of-a-simply-connected-locally-path-connected-cl – Math_tourist Nov 22 '19 at 14:21