Fundamental group of $\mathbb{R}P^2\#\mathbb{R}P^2$ using Van Kampen theorem

Asked Nov 18 '19 at 11:32

Active Nov 19 '19 at 11:34

Viewed 399 times

I know that $\mathbb{R}P^2\#\mathbb{R}P^2$ is Klein's bottle but I don't want to go that way. I wish to find it using Van Kampen's theorem. I made the diagram as shown below. The fundamental group of this open subset of the connected sum is $\mathbb{Z}$ and it is generated by $ab$. The intersection of the two open subsets deformation retracts to a circle; its fundamental group generated by $w$, say.

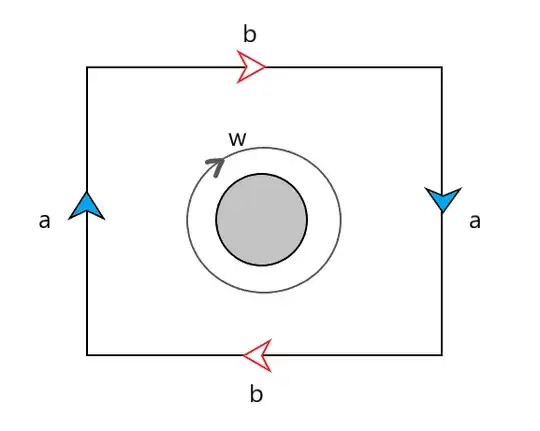
Then $i_{1,2}(w)=abab$. Similarly $i_{2,1}(w)=cdcd$. Then the fundamental group should be $\langle ab,cd:(ab)^2=(cd)^2\rangle$, which is not the fundamental group of Klein bottle. So what went wrong here?

asked Nov 18 '19 at 11:32

Smooth Alpert Frame

3,290

Please tell us what you think the fundamental group of the Klein bottle is. – JWL Nov 19 '19 at 12:31
@JWL it should be $\langle a,b:ab=ba^{-1}\rangle$ – Smooth Alpert Frame Nov 19 '19 at 12:33
1

That presentation is equivalent to $\langle ab, b : (ab)^2 = b^2 \rangle$, so you have the correct fundamental group above. – JWL Nov 19 '19 at 12:35
I didn't realize that. Thank you! – Smooth Alpert Frame Nov 19 '19 at 12:51

Fundamental group of $\mathbb{R}P^2\#\mathbb{R}P^2$ using Van Kampen theorem

0 Answers0