Extra terms in Fourier series estimate

Question

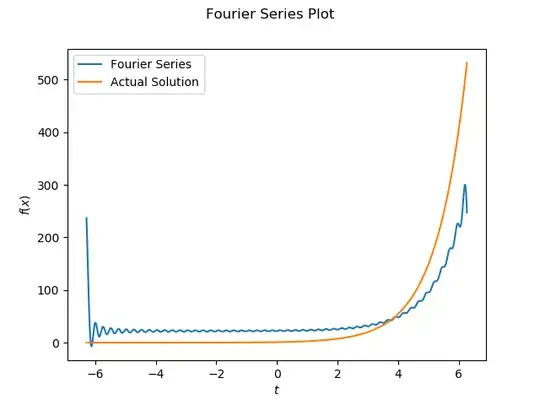
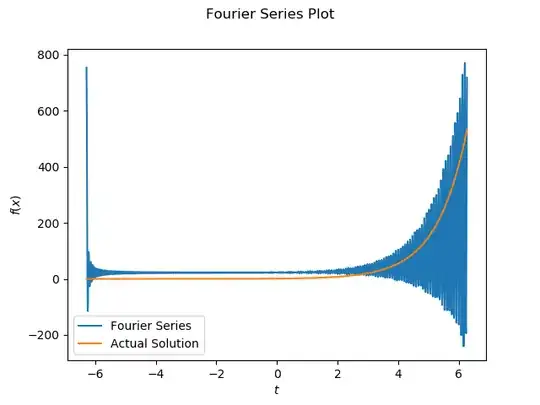
Is there any reason why adding more and more terms to a Fourier Series representation of a function would cause any wierdness?

I was under the impression that, in general, a smooth function can be perfectly represented by a Fourier Series given an infinite number of terms.

However, when I programmed a small algorithm to compute and graph a Fourier series for $e^x$, I noticed that if I added too many coefficients, things started to get really crazy. Here, for example are plots with 50 terms and 200 terms. For both of these, the Fourier coefficients $c_n$ were calculated for $x$ in the interval $[-2 \pi, 2 \pi]$ using trapezoid rule with $h = 0.025$:

Answer 1

These oscillations are called the Gibbs phenomenon. Your solution should be periodic and smooth to have good Fourier approximations. Here, when you look at your function as a periodic one, you have a huge discontinuity in $2\pi$.

UPDATE1:

If I were you, I would try either a cosine expansion (your function is defined on $[-6\pi,2\pi]$ by setting: $$f(-2\pi-x)=f(-2\pi+x)$$ and see what I've got.

Or compute: $$ \mathcal{F}\Biggl(f(x)-\left[f(-2\pi)+(x+2\pi)\frac{f(2\pi)-f(-2\pi)}{4\pi}\right]\Biggr), $$ where $\mathcal{F}$ is my fourier transform, do my trucation, and compute the inverse transform: $$ \mathcal{F}^{-1}(\hat{g})+\left[f(-2\pi)+(x+2\pi)\frac{f(2\pi)-f(-2\pi)}{4\pi}\right] $$

These are two way to make the discontinuity disappear, the first one being canonical.