1

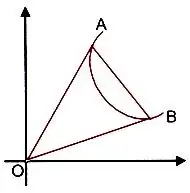
Consider this figure:

enter image description here

Here the curve $AB$ is given by $s$, $$s = ax^2 + by^2 + 2hxy + 2gx + 2fy + c = 0 \tag1$$

If equation of line $AB$ is $L$, then, $$L = lx + my + n = 0 \tag2$$

To find the equation of pair of straight lines $OA$ and $OB$, we use the method of homogenization of second degree equation i.e., from $(1)$,

$$s = ax^2 + by^2 + 2hxy + 2gx(1) + 2fy(1) + c(1)^2 = 0 \tag3$$

From $(2)$, $$\frac{lx + my}{-n} = 1 \tag4$$

Now substituting $(4)$ in $(3)$,

$$ax^2 + by^2 + 2hxy + 2gx\left(\frac{lx + my}{-n}\right) + 2fy\left(\frac{lx + my}{-n}\right) + c\left(\frac{lx + my}{-n}\right)^2 = 0 \tag5$$

This way we can homogenize the equation. Homogenizing equation $(1)$ gives us the equation of pair of straight lines $OB$ and $OA$.

My question is how does equation $(5)$ represent the equation of pair of straight lines?

I know that the pair of straight lines passing through the origin are homogenized equation. But how does equation $(5)$ represent that?

Is it like:

The equation

  • satisfies the point of intersection $A$ and $B$
  • is homogeneous i.e. it must be a pair of straight lines passing through the origin

Due to the above reasons we can conclude that the equation is of the pair of straight lines $OA$ and $OB$. Is it?

These were the same reasons as provided in another post.

After checking that post, another question struck my mind. Isn't the equation of the curve and the pair of straight line the same as we only substitute equation $(4)$ instead of $1$ ? If yes, how can this be the case?

Kaushik
  • 866
  • 1
    I would plug in $$y=-\frac{x+n}{m}$$ into the equation $$ax^2+by^2+2hxy+2yx+2fy+c=0$$ – Dr. Sonnhard Graubner Oct 31 '19 at 08:31
  • 1
    $(1)$ is not the same as $(5)$. Note that $(4)$ holds only for the points on the line $AB$. – mathlove Oct 31 '19 at 09:28
  • So when we substitute $(4)$ in it, we form an equation such that the points must lie on $AB$ which is different from $(1)$. Is it? I think it is not yet clear. Could you please write an elaborate answer for the last question? – Kaushik Oct 31 '19 at 09:36
  • 1
    Consider a point $X(x_0,y_0)$ on $(1)$ satisfying $X\not=A$ and $X\not=B$. Since $X$ is not on the line $AB$, we see that $\frac{lx_0+my_0}{-n}$ is not equal to $1$, which implies that $X$ is not on $(5)$. So, $(1)$ is not the same as $(5)$. – mathlove Oct 31 '19 at 10:16
  • @mathlove So is it like we are reducing the possible $(x,y)$ solutions. $(1)$ had a larger solution set $(x,y)$. But know as we use $(4)$ in it, the solution set is such that it should also satisfy equation $(4)$. Is it? – Kaushik Oct 31 '19 at 12:41
  • According to my understanding, when we add equation $(4)$ to equation $(1)$, what we are doing is that we are confining the solution set to point $(x,y)$ such that it lies on $(4)$. Now as the the equation became homogeneous, it must be that of a pair of straight lines passing through origin. Moreover, as we use equation $(4)$ in it, $A$ and $B$ must satisfy both equation $(5)$ and $(4)$. Is it correct? – Kaushik Oct 31 '19 at 12:47
  • Are you saying that all the points on $(4)$ satisfy $(5)$? – mathlove Oct 31 '19 at 12:54
  • No, the points that satisfy $(5)$ must satisfy $(4)$. – Kaushik Oct 31 '19 at 13:05
  • Let us continue this discussion in chat. – Kaushik Oct 31 '19 at 13:05

4 Answers4

1

Hint.

Considering

$$ a x^2+b x y + c y^2 = (c_1 x+ c_2 y)(c_3 x + c_4 y) $$

identifying coefficients we get

$$ \cases{ a=c_1 c_3\\ b = c_1c_4+c_2c_3\\ c=c_2c_4 } $$

now solving for $c_1,c_2,c_3$ we have

$$ \cases{ c_1 = \frac{b c_4\pm|c_4|\sqrt{b²-4ac}}{2c_4^2}\\ c_2 = \frac{c}{c_4}\\ c_3 = \frac{b c_4\pm|c_4|\sqrt{b^2-4ac}}{2c} } $$

so the condition for a pair of lines is

$$ b^2-4 a c \ge 0 $$

Cesareo
  • 36,341
0

Since in Eq. (5), the sum of powers of $x$ and $y$ is 2, so it is a homogenous equation of degree 2, notice there is no constant added in it. A homogeneous quadratic may represent just point, pair of real straight lines passing through origin or nothing. $$ \mbox{A point:}~~~x^2+y^2=0 \implies x=0, y=0$$ $$\mbox{A pair of stright lines:} ~~~ax^2+y^2+3xy=0 \implies y=m x, m_1,m_2=\frac{-3\pm \sqrt{5}}{2}.$$ $${\mbox nothing :} ~~~x^2+y^2+xy=0.$$

Z Ahmed
  • 46,319
0

The equation will only be the same if $$\frac{lx + my}{-n} = 1$$ Which is only true if the point $$(x,y)$$ lies on the line. Since we are substituting ith in the curve and for the point of intersection of the curve and the line, $$\frac{lx + my}{-n} = 1$$ and the equation of curve $$s = ax^2 + by^2 + 2hxy + 2gx + 2fy + c = 0$$ is also satisfied at that point, we are getting the pair of lines passing through the points and the origin.

Aarush Saharan
  • 727
-1

Doing so we get $$ax^2+b\left(-\frac{lx+n}{m}\right)^2+2hx\left(-\frac{lx+n}{m}\right)+2x\left(-\frac{lx+n}{m}\right)+2f\left(-\frac{lx+n}{m}\right)+c=0$$ This equation can be solved for $x$.

Dr. Sonnhard Graubner
  • 97,058
  • But how is this the equation of pair of straight lines $OA$ and $OB$? – Kaushik Oct 31 '19 at 08:41
  • $OA$ or $OB$ has the equation $y=m_1x$ or $y=m_2x$ – Dr. Sonnhard Graubner Oct 31 '19 at 08:43
  • 1
    I think you didn't understand my question. Could you please explain the following line first: 'Isn't the equation of the curve and the pair of straight line the same as we only substitute equation $(4)$ instead of $1$ ? If yes, how can this be the case?' – Kaushik Oct 31 '19 at 08:45
  • Or maybe I didn't understand what you're trying to say. Could you please elaborate? – Kaushik Oct 31 '19 at 08:57
  • @DrZafarAhmedDSc So it doesn't represent the equation of pair of straight lines passing through origin, right? It is also not homogenized because of $-\frac{2xn}{m}$ and other terms similar to that. Isn't? – Kaushik Oct 31 '19 at 09:57
  • @Kaushik: Note that the equation in this answer is different from $(5)$. This answer set $y=-\frac{lx+n}{m}$, which is not what you did. – mathlove Oct 31 '19 at 10:28