On the direction of steepest ascent of a plane in $\mathbb{R}^3$.

Asked Oct 30 '19 at 12:37

Active Oct 30 '19 at 12:37

Viewed 154 times

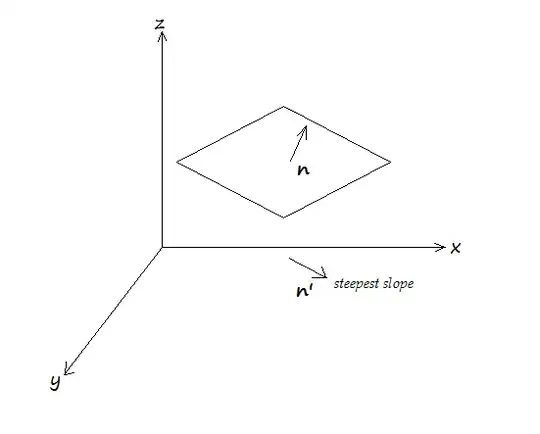
Suppose we have a plane in $\mathbb{R}^3$ whose equation is given by $$z=ax+by,$$

and let $\textbf{n}(-a,-b,1)$ be a vector normal to this plane.

How can we intuitively explain why the projection of $\textbf{n}$ onto the $xy$-plane, $\textbf{n}'(-a,-b)$, points toward the steepest slope (with respect to a point in the $xy$-plane)?

asked Oct 30 '19 at 12:37

Hilbert

1

See the first full paragraph of this answer for a way to visualize this. – amd Oct 31 '19 at 23:36
My question was partly inspired by your answer, I couldn't really understand the cylinder explanation. – Hilbert Oct 31 '19 at 23:40
1

For another way to visualize it, try this other answer, in which the tangent plane to a surface is intersected by a various vertical planes. – amd Oct 31 '19 at 23:41
Thank you, the second answer was exactly what I was looking for. – Hilbert Nov 01 '19 at 00:03

On the direction of steepest ascent of a plane in $\mathbb{R}^3$.

0 Answers0