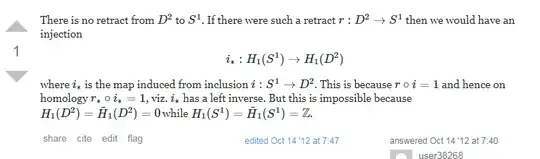0

There is no retraction map from unit disk to its boundary.

I was reading this proof:

enter image description here

It is found here in this link Retraction map from unit disk to its boundary

But I do not understand why the map $i_{*}$ is an injection, could anyone explain this for me please?

Also if someone could write for me a more clear proof than this, it will be greatly appreciated.

  • 1
    $r \circ i =1 \implies {(r \circ i)}* = 1* \implies r_* \circ i_* = 1 $ So $i_$ has a left inverse! and thus is injective! (Since, for all $x,y$ , $i_ (x)= i_* (y) \implies r_* \circ i_* (x)= r_* \circ i_* (y) \implies x=y)$ – Brozovic Oct 04 '19 at 16:58
  • so why the induced map is an injection? @Brozovic –  Oct 04 '19 at 16:59

1 Answers1

2

Your hypothesis is that there is a section $i$ of $r$, that is, $r \circ i$ is the identity $1_{S^1}$ of $S^1$. Then it holds that $(r \circ i)_*=(1_{S^1})_*$. Moreover, the following two equalities hold:

$(1)$ $(r\circ i)_*=r_* \circ i_*$

$(2)$ $(1_{S^1})_*=1_{H_1(S^1)}$

Indeed, the functional relation sending a continuous map $f\colon S \to T$ to $f_* \colon H_1(S) \to H_1(T)$ is a functor and the request that $(1)$ and $(2)$ hold is precisely the definition of the notion of functor.

It follows that $r_* \circ i_*=1_{H_1(S^1)}$. Hence $i_*$ is injective.

Matteo Spadetto
  • 1,551