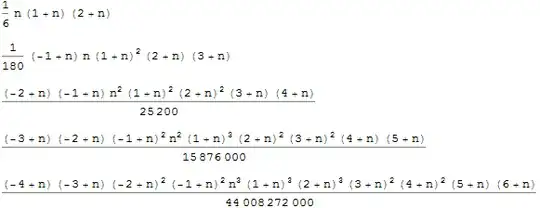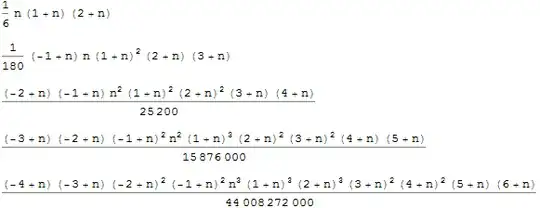16

Given positive integers $n$ and $d$, where $d\geq 2$, I would like to compute the sum $$\displaystyle\sum_{0\leq i_{1} < i_{2} < ... < i_{d}\leq n} \quad\displaystyle\prod_{1 \leq p < q \leq d}\left(i_{q} - i_{p}\right).$$ Since there are $d\choose 2$ factors in the product, the sum should return a polynomial in $n$ of degree $d(d+1)/2$. Ideally I would like to know all coefficients of the polynomial in $n$. The leading coefficient (i.e., coefficient of $n^{d(d+1)/2}$) is of particular interest.

For example, when $d=2$, our sum becomes $\displaystyle\sum_{i=0}^{n}\displaystyle\sum_{j=i+1}^{n}(j-i) = \frac{1}{6}n(n+1)(n+2)$, and the leading coefficient (of $n^3$) is $1/6$.

When $d=3$, our sum gives $\displaystyle\sum_{i=0}^{n}\displaystyle\sum_{j=i+1}^{n}\displaystyle\sum_{k=j+1}^{n}(k-j)(j-i)(k-i) = \frac{1}{180}(n-1)n(n+1)^{2}(n+2)(n+3)$, and the leading coefficient (of $n^{6}$) is $1/180$.

For $d=4$, WolframAlpha gives $$\displaystyle\sum_{i=0}^{n}\displaystyle\sum_{j=i+1}^{n}\displaystyle\sum_{k=j+1}^{n}\displaystyle\sum_{l=k+1}^{n}(l-k)(l-j)(l-i)(k-j)(k-i)(j-i)\\ = \frac{1}{25200}(n-2)(n-1)n^{2}(n+1)^{2}(n+2)^{2}(n+3)(n+4)$$ and the leading coefficient (of $n^{10}$) is $1/25200$.

I am not sure if this object is well-known, or has a name. Any references will be great too.

Abhishek Halder
  • 1,195
  • 3
    Extending to $d = 0$ using the empty product gives a sum of $n$, and even with this extension the sequence of ratios $1, \frac{1}{6}, \frac{1}{30}, \frac{1}{140}$ of successive leading coefficients follows the pattern $\frac{n!^2}{(2n+1)!}$. – Travis Willse Sep 27 '19 at 21:43
  • 3
    And the reciprocals of these ratios, $\frac{(2n+1)!}{n!^2}$, is OEIS A002457 – rogerl Oct 02 '19 at 19:02
  • 2
    If your primary interest is the leading coefficient, you should be able to replace all the sums by integrals (so that, e.g. the $d=4$ case becomes $$\int_0^1 \int_0^w \int_0^x \int_0^y (w-x)(w-y)(w-z)(x-y)(x-z)(y-z) , dz , dy , dx , dw=\frac{1}{25200}.$$ Effectively this is the expected product of the pairwise distances of $d$ randomly placed points in the unit interval, and it feels like in this language it should have been studied somewhere (I don't have a reference though). – Kevin P. Costello Oct 02 '19 at 19:25
  • 1
    @Kevin: I was thinking along similar lines: the Faulhaber's formula gives $\sum_{k=1}^{p}k^{p} = \frac{1}{p+1}n^{p+1} + O(n^{p})$. When we use this in the nested sum, there are many terms contributing to the leading coefficient .... not sure if there is a good way to keep track of them so as to get the leading coefficient as function of $d$. – Abhishek Halder Oct 03 '19 at 00:56

2 Answers2

5

In terms of the leading term coefficient the following identities hold true: \begin{eqnarray} c_d&=&\int\limits_{0 \le x_1 \le \cdots x_d \le 1} \prod\limits_{1 \le p < q \le d} (x_p - x_q)\cdot \prod\limits_{p=1}^d dx_p\\ &=&\sum\limits_{\sigma \in \Pi} \mbox{sign($\sigma$)} \frac{1}{\prod\limits_{i=1}^d \sum\limits_{j=1}^i \sigma_j} \quad (1)\\ &=& \int\limits_{[0,1]^d} \left(\prod\limits_{p=1}^d x_p^{\binom{p}{2}+p-1} \right) \cdot \prod\limits_{p=1}^d \prod\limits_{q=p+1}^d \left(1-\prod\limits_{\xi=p}^{q-1} x_\xi\right) \cdot \prod\limits_{p=1}^d d x_p \quad (2) \\ &\underbrace{=}_{?}& \prod\limits_{\xi=1}^{d-1} \frac{(\xi!)^2}{(2 \xi+1)!} \end{eqnarray} where in $(1)$ we expanded the Vandermonde determinant in a sum over permutations $\Pi$ and then integrated term by term and in $(2)$ we we used the trick $1/p = \int\limits_0^1 x^{p-1} dx$ and the definition of the Vandermonde determinant again. The representations above are readily used to compute the result for $d \le 9$. We have:

In[484]:= d =.;
ss = Table[
  Total[Signature[#] Product[1/(Total[Take[#, i]]), {i, 1, d}] & /@ 
    Permutations[Range[1, d]]], {d, 1, 9}]
Table[Expand[
   Product[x[p]^(Binomial[p, 2] + p - 1), {p, 1, 
      d}] Product[(1 - Product[x[xi], {xi, p, q - 1}]), {p, 1, d}, {q,
       p + 1, d}]] /. x[n_]^p_. :> 1/(p + 1), {d, 1, 9}]
Table[Product[(xi!)^2/(2 xi + 1)!, {xi, 1, d - 1}], {d, 1, 9}]

enter image description here

Update: Let us denote: \begin{eqnarray} {\mathcal S}_d^{(n)} := \sum\limits_{0 \le i_1 < i_2 < \cdots < i_d \le n} \prod\limits_{1 \le p < q \le d} (i_q-i_p) \end{eqnarray} for $n \ge d-1$. Then my conjecture is the following: \begin{eqnarray} {\mathcal S}_d^{(n)} = \left[\prod\limits_{\xi=1}^{d-1} \frac{(\xi!)^2}{(2 \xi+1)!}\right] \cdot \left[\prod\limits_{j=-d+1}^1 (n+j)^{\lceil \frac{j+d-1}{2} \rceil}\right] \cdot (n+2)^{\lfloor \frac{d}{2}\rfloor} \cdot \left[\prod\limits_{j=3}^d (n+j)^{\lceil \frac{d-j+1}{2} \rceil }\right] \end{eqnarray}

I have verified this conjecture for $d \le 6$ using the code below:

d = 2; Clear[a]; Clear[aa]; i[0] = 0;
aa = Table[a[p], {p, 0, d - 1}];
smnD = Product[i[q] - i[p], {p, 1, d}, {q, p + 1, d}];
subst = First@
    Solve[CoefficientList[
       smnD - (Sum[Binomial[i[d] - i[d - 1], p] a[p], {p, 0, d - 1}]),
        i[d]] == 0, aa] // Simplify;
(*Sum over i[d] done.*)
S = Sum[Binomial[n + 1 - i[d - 1], p + 1] a[p], {p, 0, d - 1}] /. 
   subst;
upLim = d - 1;
For[count = 1, count <= d - 1, count++,
  upLim = upLim + d - count;
  aa = Table[a[p], {p, 0, upLim}];
  subst = 
   First@Solve[
      CoefficientList[
        FunctionExpand@(S - (Sum[
             Binomial[i[d - count] - i[d - count - 1], p] a[p], {p, 0,
               upLim}])), i[d - count]] == 0, aa] // Simplify;
  (*Sum over i[d-count] done.*)
  S = Sum[
     Binomial[n + 1 - i[d - count - 1], p + 1] a[p], {p, 0, 
      upLim}] /. subst;
  Print["count=", count, "done"];
  ];
Factor[FunctionExpand@S]

enter image description here

Przemo
  • 11,971
  • 1
  • 25
  • 56
  • I think the coefficient of $\mathrm{sign}(\sigma)$, i.e. $\int \prod x_j^{\sigma_j-1} dx$, should be $(\prod_{j=1}^n \sum_{i=1}^j \sigma_i)^{-1}$, not $(\sum \sigma_j)^{-1}$, right? – user125932 Oct 04 '19 at 16:19
  • Yes, yes, of course, I am sorry for that. I fixed it. – Przemo Oct 04 '19 at 17:07
  • This looks nice, but my impression is that the polynomial factors completely into linear terms, and that probably cannot be proven by an integral approximation, can it? – darij grinberg Oct 05 '19 at 02:58
  • 1
    @darij grinberg It is indeed quite remarkable that this factorizes so nicely. I have updated my answer and provided a Mathematica code that computes the sum for higher values of $d$. By the way , why are you interested in this very problem ? – Przemo Oct 07 '19 at 11:54
  • 1
    I care partly because the sum is the sum of all maximal minors of the Vandermonde-like rectangular matrix $\left(i^{j-1}\right)_{1\leq i\leq n,\ 1\leq j\leq d}$, and it appears that there may be a more general determinant identity behind it. Also, the sum can be reinterpreted as counting something like Gelfand-Tsetlin patterns, since each $i_q - i_p$ factor can be viewed as choosing an integer from the interval $\left[i_p,i_q\right)$. These are not quite Gelfand-Tsetlin patterns, because all these integers in a given addend of the sum are independent, but close enough to be interesting to me. – darij grinberg Oct 07 '19 at 13:18
  • Not a proven answer, but getting the exponents figured out is well worth the bounty. Congrats! – darij grinberg Oct 10 '19 at 00:26
  • This is obvious from the context but just wanted to make sure: the second \prod in (2) should run from $p=1$ to $d-1$. I am still unable to prove the last equality (with question mark) for $c_{d}$. Posted in MathOverflow with links to this page. – Abhishek Halder Nov 04 '19 at 17:35
1

This is a follow up on Przemo's answer in deriving the final expression of the leading coefficient $c_{d}$. Notice that $d! c_{d}$ equals the Vandermonde determinant integrated over $[0,1]^{d}$. In an 1955 paper by De Bruijn (see toward the end of Sec. 9), it is proved that

$$\int_{[0,1]^{d}}\prod_{1\leq i < j \leq d} |x_{i} - x_{j}| \: {\rm{d}}x_{1} ... {\rm{d}}x_{d} = \frac{\{1! \times 2! \times 3! \times ... \times (d-1)!\}^{2} d!}{1!\times 3! \times 5! \times ... \times (2d-1)!}.$$

That proof utilizes the result (also derived in that paper) that integrals of this type are equal to certain Pfaffian form. Equating the above with $d! c_{d}$ recovers the expression conjectured by Przemo:

$$c_{d} = \prod\limits_{\xi=1}^{d-1} \frac{(\xi!)^2}{(2 \xi+1)!}.$$

Abhishek Halder
  • 1,195