2

2. Let $\alpha$ be a constant $\neq {-c}$. Find the solution $u(x,t)$ of (4.1) in the quadrant $x>0, t>0$, for which $$ \begin{aligned} u &= f(x), \qquad u_t = g(x)\quad \text{for } t=0, x>0\\ u_t &= \alpha u_x, \quad \text{for } x=0, t>0, \end{aligned} $$ where $f$ and $g$ are of class $C^2$ for $x>0$ and vanish near $x=0$. (Hint: Use (4.5)). Show that generally no solution exists when $\alpha = {-c}$.

The equations are $$u_{tt}-c^2u_{xx}=0 \tag{4.1}$$ and $$u(x,t)=F(x+ct)+G(x-ct). \tag{4.5}$$

What I tried :

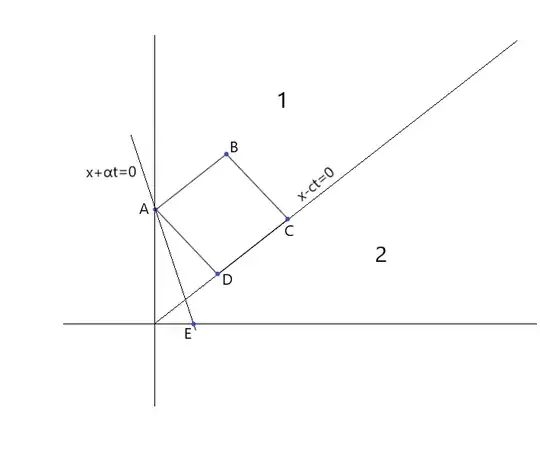
On region $2$ I will have the solution directly from D'Alembert's formula. For any point $B$ in region $1$ I can draw parallelogram with sides having slopes $c,-c$ as shown below. I have : $u(B)+u(D)=u(A)+u(C)$ by parallelogram property. I only need to know $u(A)$ which lies on the $t$-axis. attempt

On $t$-axis $u$ satisfies $u_t=\alpha u_x$. If $u$ satisfied this on a region I could have, for instance, drawn lines parallel to $x+\alpha t=0$ through $A$ and wherever it cut the $x$-axis, the value of $u$ at that point would have given the value at $A$ (since $u$ would be constant along that line). But that is not the case. What can I do from here?

EditPiAf
  • 21,328
Smooth Alpert Frame
  • 3,290

1 Answers1

2

Let us introduce $p = u_x + u_t/c$ and $q = -u_x + u_t/c$ (see e.g. (1) chap. 12-*). From the PDE, we deduce $p_t = c p_x$ and $q_t = -c q_x$, i.e. two linear advection equations with speed $\mp c$ are obtained. The characteristic curves along which $p$, $q$ are constant are straight lines with slope $\mp c$ in the $x$-$t$ plane.

  • if $0< c t < x$ (zone 2 in OP), then integration of $u_t = \frac{c}2 (p+q)$ with $$p(x,t) = f'(x+ct) + \frac{g(x+ct)}c \quad\text{and}\quad q(x,t) = -f'(x-ct) + \frac{g(x-ct)}{c}$$ w.r.t. $t$ leads to d'Alembert's formula: $$ u(x,t) = \frac{1}{2}(f(x-ct) + f(x+ct)) + \frac{1}{2c}\int_{x-ct}^{x+ct} g(\xi)\, \text d\xi \, . $$

  • if $0< x < c t$ (zone 1 in OP), we proceed similarly. The expression of $p$ is unchanged, but the expression of $q$ is deduced from the interaction of the characteristics with the boundary $x=0$. On the one hand, the $-c$ characteristics give $p(0,t) = f'(ct) + g(ct)/c$ at $x=0$. On the other hand, we deduce $p(0,t)=\frac{\alpha+c}{\alpha - c}q(0,t)$ from the boundary condition, which is compatible with the previous expression of $p(0,t)$ unless $\alpha = -c$. Following the characteristics, we have $q(x,t) = q(0,t-x/c)$. Then, integration of $u_t = \frac{c}2 (p+q)$ for $t>x/c$ yields the solution in the whole domain.

(1) R. Habermann, Applied Partial Differential Equations: with Fourier Series and Boundary Value Problems, 5th ed. Pearson Education Inc., 2013.

EditPiAf
  • 21,328
  • How did you get $q(x,t)=q(0,t−x/c)$? Is $q$ constant along that line? I thought the solution to $-u_x+u_t/c$ is constant along characteristic lines? – Smooth Alpert Frame Nov 20 '19 at 15:36
  • @HritRoy Yes, $q = -u_x + u_t/c$ is constant along that line. I may add a picture of the configuration in the following days if I get the time to do so – EditPiAf Nov 22 '19 at 11:38