0

Could someone please give me a method of deriving part of this table?

This is used in numerical methods, the forward finite difference method. I've spent a few days working on this, but, my answers did not fit the table. I need an example, of how to derive the third and fourth derivatives enter image description here

Please

Arukana Koto
  • 1

1 Answers1

0

Using the Taylor shift operator, you have that $$ [\Delta f](x)=f(x+h)-f(x)=[(e^{hD}-1)f](x)=[hD(1+\tfrac12hD+\tfrac16h^2D^2+...)f](x) $$ To compute forward approximations of the derivatives, you want to invert this relation, express $D$ in terms of $Δ$. This is just a Taylor series inversion problem for $$ u=e^v-1\implies v=\ln(1+u)=u-\tfrac12u^2+\tfrac13u^3\mp\dots $$ That means that to compute the $n$-th forward derivative to order $p$ you need to evaluate $$ D^n=h^{-n}(\ln(1+Δ+O(Δ^{p+1}))^n $$ treating $Δ$ as variable, then truncate and expand $Δ$ in terms of the shift operator, $Δ=S-1$ where $[Sf](x)=f(x+h)$.

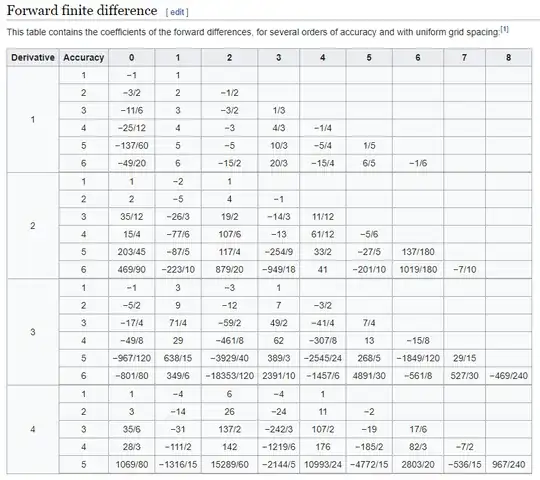
Using a CAS script (Magma, try it out)

P<S>:=PowerSeriesRing(Rationals());
for n in [1..5] do
  for p in [1..3] do
    n,p,Evaluate(Truncate(Log(1+S+O(S^(p+1)))^n),S-1);
  end for;" ";
end for;

gives the table

1 1 -1 + S
1 2 -3/2 + 2*S - 1/2*S^2
1 3 -11/6 + 3*S - 3/2*S^2 + 1/3*S^3

2 1 1 - 2*S + S^2
2 2 2 - 5*S + 4*S^2 - S^3
2 3 35/12 - 26/3*S + 19/2*S^2 - 14/3*S^3 + 11/12*S^4

3 1 -1 + 3*S - 3*S^2 + S^3
3 2 -5/2 + 9*S - 12*S^2 + 7*S^3 - 3/2*S^4
3 3 -17/4 + 71/4*S - 59/2*S^2 + 49/2*S^3 - 41/4*S^4 + 7/4*S^5

4 1 1 - 4*S + 6*S^2 - 4*S^3 + S^4
4 2 3 - 14*S + 26*S^2 - 24*S^3 + 11*S^4 - 2*S^5
4 3 35/6 - 31*S + 137/2*S^2 - 242/3*S^3 + 107/2*S^4 - 19*S^5 + 17/6*S^6

5 1 -1 + 5*S - 10*S^2 + 10*S^3 - 5*S^4 + S^5
5 2 -7/2 + 20*S - 95/2*S^2 + 60*S^3 - 85/2*S^4 + 16*S^5 - 5/2*S^6
5 3 -23/3 + 295/6*S - 135*S^2 + 1235/6*S^3 - 565/3*S^4 + 207/2*S^5 - 95/3*S^6 + 25/6*S^7

which replicates the cited coefficient table.

Lutz Lehmann
  • 131,652