Pre-calculus method for finding the 'neat' value $\sin(\frac{\pi}{3})=\frac{\sqrt3}{2}$?

Question

If you have a unit circle and the Pythagorean theorem, how do you discover that $\sin(\frac{\pi}{3})=\frac{\sqrt3}{2}$? Finding the $1, 1, \sqrt2$ triangle seems more obvious. Do you consult a chart of previously-found Pythagorean triples and scale them to a unit hypotenuse? Do you have some reason (and, if so, what?) for wanting to know the sine whose cosine $=\frac{1}{2}$ and get lucky with a neat (as long as you don't mind surds) value? Do you use lengthy trial and error (historically, over centuries)? Or is there some other pre-calculus method than Pythagoras?

Answer 1

The commonly-known "special" angles of this kind go so far back into antiquity that I suspect it is very hard to say how people first figured them out.

The $3,4,5$ Pythagorean triple was allegedly discovered very long ago, probably by trial and errors. But the interesting thing about Pythagorean triples in ancient times was that they give you a triangle with a known right angle. The other two angles of such a triangle would not have been as interesting.

At some point people became interested in things such as how to construct geometric figures using methods such as straightedge and compass. The construction of a $\frac12, \frac{\sqrt3}2, 1$ triangle is especially simple and could very likely be discovered when you were pursuing some other line of inquiry entirely.

For example, suppose we want to bisect the line segment $AB.$ Put one point of your compass at $A$ and make a circle with center $A$ passing through $B.$ Now put one point at $B$ and make a circle with center $B$ passing through $A.$ Let the two intersections of those two circles be named $C$ and $D.$ Let the intersection of the line $CD$ with the line $AB$ be a point named $M.$ Then $M$ is the midpoint of the segment $AB.$

Now if you were an ancient Greek playing with such constructions it might be interesting to you to observe that the points $A,$ $B,$ and $C$ are all equidistant from each other and are the vertices of an equilateral triangle. Therefore all three internal angles of $\triangle ABC$ are equal. But since the sum of angles of any triangle is $\pi,$ each of the angles must be $\frac\pi3.$

Also, $CD$ is perpendicular to $AB,$ so $\triangle AMC$ is a right triangle with a right angle at $M.$ But the angle $MAC$ is the same as $BAC,$ that is, it is $\frac\pi3.$ So now we know all the angles of $\triangle AMC$. (The remaining angle is what is needed to sum to $\pi,$ that is, it is $\frac\pi6.$)

We observe that since $M$ is the midpoint of $AB$ and since $\lvert AB\rvert = \lvert AC\rvert,$ then $\lvert AM\rvert = \frac12\lvert AC\rvert.$ Now all we have to do is apply the Pythagorean Theorem:

$$ \lvert AC\rvert^2 = \lvert AM\rvert^2 + \lvert CM\rvert^2 = \left(\frac12\lvert AC\rvert \right)^2 + \lvert CM\rvert^2, $$

and solving for $\lvert CM\rvert$ in terms of $\lvert AC\rvert$ we might observe that

$$ \lvert CM\rvert = \frac{\sqrt3}2 \lvert AC\rvert, $$

except that the ancient Greeks did not have all this notation of square root signs and so forth. I think they were more interested in the fact they could construct the triangle than in how to describe the numeric ratios of the side lengths, especially since $\frac{\sqrt3}2$ is irrational and therefore not the kind of number they liked to use in a ratio.

When people did get interested in writing numbers in forms like $\frac{\sqrt3}2,$ however, I'm sure it did not take long for someone to figure out that the sides of this triangle are in the ratio $\frac12, \frac{\sqrt3}2, 1,$ since the triangle was already so well known.

Also, until about the year 1800 the only angles that were known to be rational multiples of $\pi$ and were known to be expressible using square roots and elementary arithmetic were $\frac\pi2,$ $\frac\pi3,$ $\frac\pi5,$ and any other angle in a set that contains just these angles and the angles you can generate recursively by dividing an angle in the set by two or by taking the sum or difference of two angles in the set. And as I said at the start, the constructions of those angles are very, very old.

Answer 2

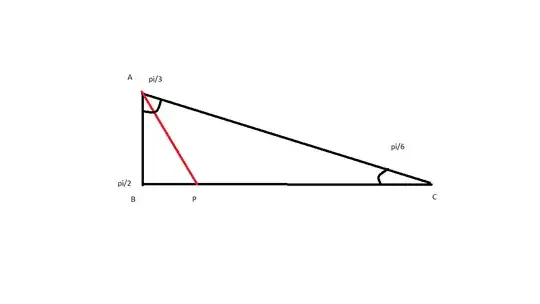
Yes, I (literally) just came up with one for the $\displaystyle \frac{\pi}{6}, \frac{\pi}{3}, \frac{\pi}{2}$ special triangle over the last minute. The elementary proof involves nothing more than Pythagoras' theorem, similar triangles and the angle bisector theorem (which can be proven without trigonometry, using just an area-based argument).

Consider the right angled triangle $ABC$ with right angle at $B$ as in the diagram. Angles are as indicated. Let $AB = 1, BC = x$. Deduce that $\displaystyle CA = \sqrt{1+x^2}$ by Pythagoras' Theorem. Construct the angle bisector of $\angle CAB$ and let the point where it meets $BC$ be $P$. Note that $\displaystyle \angle BAP = \frac{\pi}{6}$, and that $BP:BC = BA:CA$, so $BP = \displaystyle \frac{x}{1+\sqrt{1+x^2}}$ You now note (from the similarity of triangles $\triangle BAP$ and $\triangle BCA$) that $BP:BA = BA:BC$, giving you $\displaystyle \frac {x}{1+ \sqrt{1+x^2}} = \frac 1x$and after a bit of rearrangement you get the biquadratic $\displaystyle (x^2-1)^2 = 1 + x^2$, which has the non-trivial solution $x=\sqrt 3$. So now you can figure out the dimensions as $1, \sqrt 3, 2$, from which all the relevant trig ratios immediately follow, including the one you asked about, $\displaystyle \sin \frac{\pi}{3} = \frac{\sqrt 3}{2}$.

A brief addendum. I believe this argument is only as complicated as it needs to be (when starting with the right triangle). Note that a simple Pythagoras plus similar triangles approach is "doomed to failure" since any right angled triangle can have another two smaller and similar right triangles constructed within like this. What makes $\displaystyle \frac{\pi}{3}$ "special" here is that it can be exactly bisected to give its complement $\displaystyle \frac{\pi}{6}$, and I exploited that in my proof.

EDIT: A much simpler proof can be constructed when you begin with an equilateral triangle (constructible polygons were mentioned by @EthanBolker in a comment to another answer) and proceed to bisect it equally into two congruent right triangles (which have the required special angles). If the equilateral side length is $2$, one cathetus is $1$, and the other is $\sqrt 3$ by Pythagoras'. This immediately gives the required ratios. I have made a simple diagram below in case you have difficulty visualising this. I am retaining the above longer proof as another way of approaching the problem.

I assume you have no issues with the $1,1,\sqrt 2$ triangle that gives you $\displaystyle \sin \frac{\pi}{4} = \cos\frac{\pi}{4} = \frac{1}{\sqrt 2}$.

Answer 3

Standing on the shoulders of the other answerers, here's an image I made which could have been made by anyone with a compass and straightedge and some patience over the last few millennia.

It shows a mandala comprising: a circle (black); two squares (green and yellow); and two hexagrams (red and blue). Together the inscribed figures give all the 'neat' angles and (not labelled) all the geometric relations necessary to find the sines and cosines.

In the background are 36 (I think) auxilliary circles. Not all of them are necessary at once, but different selections of them would suffice for different combinations of inscribed shapes.

Answer 4

Many (if not all) of the 'neat' values we obtain for our six trigonometric functions come from the degree measurements $0^\circ, 30^\circ, 45^\circ, 60^\circ, 90^\circ$, as they form special triangles.

The $30, 60, 90$ triangle gives us a lot of information for our trig values. We know that the hypotenuse $=2a$, the adjacent side $=\sqrt3a$, and the remaining side $=a$.

The $45, 45, 90$ triangle gives us information as to what happens at 45 degrees.

I hope this answers your question.

Answer 5

Inspired by this post.

This post answers the question in an earlier revision: 'Pre-calculus method for finding 'neat' values of $\sin(\theta)$'.

Let's say you start with an angle of $\frac{\pi}{2}$. You bisect that angle to get $\frac{\pi}{4}$, and then measure the ratio of opposite/hypotenuse. It turns out this ratio is $\frac{1}{\sqrt{2}}$.

Let's say you start again, but with a hexagon. Joining opposite vertices together, you have managed to create $\frac{\pi}{3}$. You draw a perpendicular down from the vertex at the top, and this gives a nice opposite/hypotenuse value. You bisect $\frac{\pi}{3}$ into $\frac{\pi}{6}$, and this gives another neat value.

But now your problem is that you have to keep discovering new values of $\sin \theta$ by chance. For example, $\frac{5\pi}{12} = \frac{\pi}{6} + \frac{\pi}{4}$, but there is no neat way to find $\sin \frac{5\pi}{12}$. So you try to find an expression for $\sin(a+b)$ that uses $\sin a$ and $\sin b$.

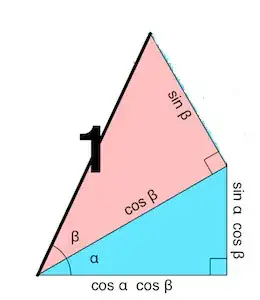
So you separate $a+b$ into two triangles with angles $a$ and $b$. You are interested in finding what the adjacent/hypotenuse ratio is. However, from the unit circle with radius or hypotenuse $1$, you can just use the fact that $\sin^2 \theta + \cos^2 \theta = 1$, so you can define $\cos \theta$ as $\sqrt{1-\sin^2 \theta}$.

You try to express the blue sides in terms of your angle. You cannot do this just with $\cos b$, but using the angle $a$ in the blue triangle, you manage this.

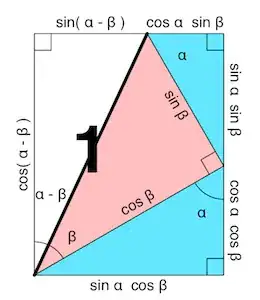
After doing the same with other triangles, making the hypotenuse of the triangles $1$ and $\sin b$, you get this diagram:

So now you discover that you can express $\sin(a-b)$ instead neatly. You get that $\sin(a-b) = \sin a \cos b - \cos a \sin b$, and to find $\sin(a+b)$, you can just substitute in $-b$.

Comparing the adjacent/hypotenuse and opposite/hypotenuse ratios of $\cos(-b)$ and $\sin(-b)$, we find that $\cos(-b) = \cos b$, and $\sin(-b) = \sin b$, so we have that $\sin(a+b) = \sin a \cos b + \sin b \cos a$. Substituting $a=b$ in the above formula, we get the double-angle formula: $\sin 2a = 2 \sin a \cos a$.

Also from the diagram, $\cos(a-b) = \cos a \cos b + \sin a \sin b$, so $\cos(a+b) = \cos a \cos b - \sin a \sin b$. Substituting $a=b$ again, we have $\cos 2a = \cos^2 a - \sin^2 a$, and using the Pythagorean identity $\sin^2 \theta + \cos^2 \theta = 1$, we have $\cos 2a = 1 - 2\sin^2 a$.

Then $\cos a = 1 - 2 \sin^2 (a/2)$, and rearranging, we find that $\sin(a/2) = ±\sqrt{\frac{1-\cos a}{2}}$: the half-angle identity.

Generalising, using these methods, you can only construct rational multiples of $\pi$. However, all of these formulas only use the four operations, and the extraction of $n$th roots, so the sines of all of these angles are algebraic numbers. This is the basis for the fact that $\sin \left( \frac{p}{q} \pi \right)$ is always algebraic when $\frac{p}{q}$ is rational (according to this post).

However, by Niven's theorem, there are only a handful of values when $\sin \theta$ is rational, namely when $\sin \theta = 0, ±\frac{1}{2}, ±1$, giving us the motivation for why we used a hexagon to calculate $\sin \frac{\pi}{6}$. The proofs for these theorems are beyond pre-calculus.