Prove that the loxodrome crosses all meridians at a constant angle

Question

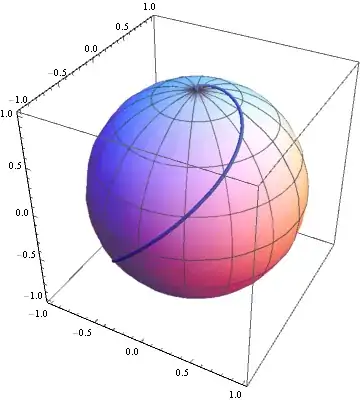
How to prove that the loxodrome (the rhumb line) crosses all meridians at a constant angle?

$$\tan\left(\frac{\pi}{4} + \frac{\psi}{2}\right) = e^{k\phi}, \quad k = \text{constant}$$

where $\psi$ is the latitude of a point on a sphere, and $\phi$ is the longitude.

A meridian is a line of latitude (so, in your notation, $\psi$ constant). — Ted Shifrin, Sep 12 '19 at 18:51
LOL ... I never use this word because it's always so confusing. Note that dictionary.com says "a circle of constant longitude passing through a given place on the earth's surface and the terrestrial poles." This is wrong, too. Constant longitude would mean a line of latitude. Ugh. — Ted Shifrin, Sep 12 '19 at 19:15
Please, help me to solve this task in the context of multivariable calculus or hint on how to approach it. — Oleh Berehovskyi, Sep 12 '19 at 19:18
Find the angle between tangent vectors to the two curves, @OlehBerehovskyi — Ted Shifrin, Sep 12 '19 at 19:18
@Rodrigo de Azevedo I checked it before and, trust me, there is no such question( — Oleh Berehovskyi, Sep 14 '19 at 07:35
@TedShifrin: Heh. It's sort of like lines parallel to the $y$-axis are given by $x=a$, I've always hated that. But, one way I remember this is that longitude lines are long. — Lee Mosher, Sep 14 '19 at 12:38
@LeeMosher: I have no problem with latitude and longitude. In my differential geometry notes, I prefer to refer to parallels and profile curves of surfaces of revolution :P — Ted Shifrin, Sep 14 '19 at 14:30

score 1 · Accepted Answer · answered Sep 14 '19 at 12:11

The stereographic projection $\sigma:\>\dot S^2\to{\mathbb R}^2$ maps the point $P\in \dot S^2$with geographical cordinates $[\psi,\phi]$ to the point $\sigma(P)\in{\mathbb R}^2$ with polar coordinates $[r,\phi]$, whereby $r$ is given by $$r={\cos\psi\over 1-\sin\psi}\ .$$ This is easily verified in a figure showing a half meridian circle of $S^2$. Writing $\tan{\psi\over2}=:t$ we therefore have $$r={{1-t^2\over 1+t^2}\over 1-{2t\over1+t^2}}={1+t\over1-t}=\tan\left({\pi\over4}+{\psi\over2}\right)\qquad\bigl(=e^{k\phi}\bigr)\ .$$ This shows that the stereographic image $\sigma(\ell)$ of your loxodrome is a logarithmic spiral $r=e^{k\phi}$ in the plane. Such a spiral intersects all radii originating at $(0,0)$ under the same angle $\alpha$ (which depends on $k$). Now these radii are just the stereographic images of the meridians on $S^2$. Since $\sigma$ is known to be conformal it follows that $\ell$ intersects all meridians on $S^2$ under the same angle $\alpha$.

Prove that the loxodrome crosses all meridians at a constant angle

1 Answers1