Since the accent in the OP is put on a purely geometric solution, i can not even consider the chance to write $\cos^2 =1-\sin^2$, and rephrase the wanted equality, thus having a trigonometric function which is better suited to geometrical interpretations.
So this answer has two steps, first we reformulate the given identity in a mot-a-mot geometric manner, the geometric framework is introduced, some strictly geometrically transposed equivalent relations are listed, then we give a proof:
In the triangle $\Delta ABC$ let $AA'$, $BB'$, $CC'$ be the heights, $A'\in BC$, $B'\in CA$, $C'\in AB$, intersecting in $H$, the orthocenter. We assume that the diameter $2R$ of the circumcircle is normed to be the unit. Then we have the following situation for the lengths of some segments in the picture:
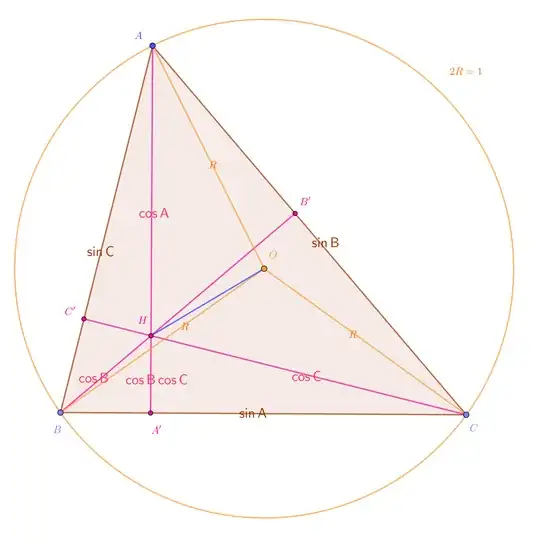
$$
\begin{aligned}
AH &=\cos A\ , \qquad & HA'&=\cos B\cos C\ ,\\
BH &=\cos B\ , \qquad & HB'&=\cos A\cos C\ ,\\
CH &=\cos C\ , \qquad & HC'&=\cos A\cos B\ .
\end{aligned}
$$
Proof: We have:
$$
\sin \hat B =\sin \widehat{C'HA}
=\frac{C'A}{AH}
=\frac{AC\;\cos A}{AH}
=\frac{2R\sin B\; \cos A}{AH}
=\frac{\sin B\; \cos A}{AH}
\ ,
$$
which implies $AH=\cos A$, and the similar relations. Then we express twice the area of $\Delta HBC$ as
$$ HA'\cdot BC =2[HBC]=HB\cdot HC\cdot \sin\widehat{BHC}\ ,$$
thus getting $HA'=\cos B\cos C$.
We are in position to give a geometric mask to the given equality:
We use the above notations in $\Delta ABC$. We denote by $a,b,c$ the lenghts of the sides. Let $M_A, M_B,M_C$ be the mid points of the sides $BC$, $CA$, respectively $AB$. Let $G=AM_A\cap BM_B\cap CM_C$ be the intersection of the medians, the centroid. Let $A^*, B^*, C^*$ be the mid points of $HA$, $HB$, $HC$. Let $N$ be the center of the Euler circle $(N)$ passing through the nine points $A',B',C'$; $M_A,M_B,N_C$; $A^*, B^*,C^*$. It is the mid point of $OH$, and $M_AA^*$, $M_BB^*$, $M_CC^*$ are diameters in $(N)$, having the lenght $R=OA=OB=OC$. (For $OM_AA^*A$ is a parallelogram.)
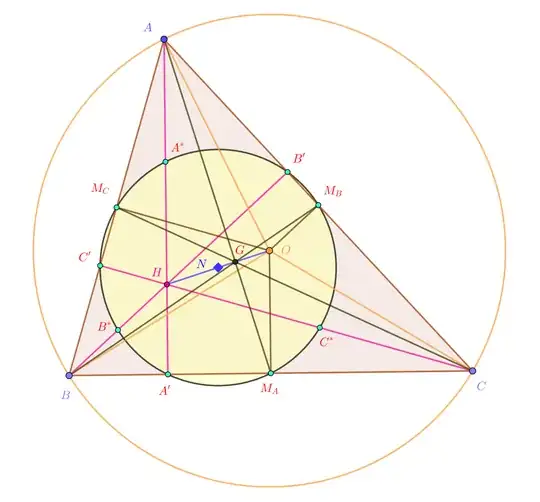
Then we have the following relations:
$$
\begin{aligned}
HA^2+HB^2+HC^2 + 2 HA\cdot HA' &= 4R^2\ ,\\
HA^*{}^2+HB^*{}^2+HC^*{}^2 + HA^*\cdot HA' &= R^2\ ,\\
4OM_A^2+4OM_B^2+4OM_C^2 &= 3R^2+OH^2\ ,\\
9R^2 &= a^2 +b^2 + c^2 +OH^2\\
9R^2 &= a^2 +b^2 + c^2 +9OG^2\ .
\end{aligned}
$$
Proof: The relations above are equivalent:
$AH^2=4A^*H^2=4OM_A^2$, and $2 HA\cdot HA'=4 HA^*\cdot HA'$ is the power of $H$ in the circle $(N)$, so it can be rewritten using its radius $NA^*=\frac 12 R$ and the distance to its center, $NH=\frac 12 OH$ as
$2 HA\cdot HA'=4 HA^*\cdot HA'=R^2-OH^2$.
From the triangle $OBM_A$,
$4OM_A^2+BC^2 =4(OM_A^2+BM_A^2)=4OB^2=4R^2$.
Note that $G$ cuts the median $AM_A$ in the proportion $AG:GM_A=2:1$, so it projects on $BC$ in the same proportion. This also holds for the colinear points $H,G,O$, so $HG:GO=2:1$, so $HO=3GO$.
The last relation, $OG^2 = R^2-\frac 13(a^2+b^2+c^2)$, is a standard formula. We have in general the formula for an arbitrary point $P$:
$$PA^2+PB^2+PC^2=GA^2+GB^2+GC^2+3GP^2\ .$$
We apply it for $P=O$, getting $3R^2=3OG^3+\sum AG^2=3OG^3+\frac 49\sum AM_A^2=3OG^3+\frac 49\sum \left(\frac 12b^2+\frac 12 c^2-\frac 14 a^2\right)=3OG^3+\frac 49\sum \frac 34a^2=3OG^3+\frac 13\sum a^2\ .$
$\square$