0

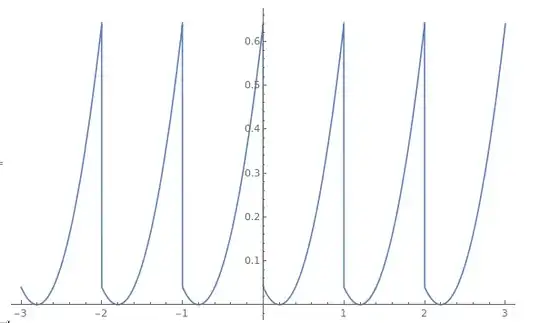
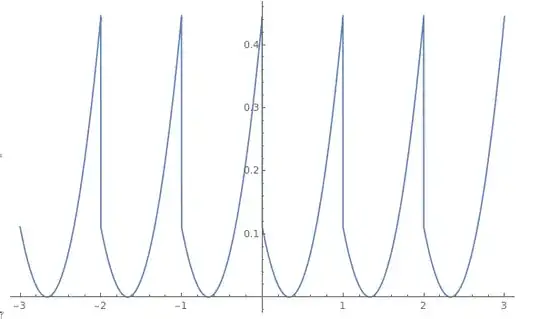
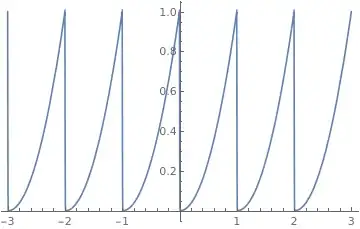
I am trying to find a periodic function, similar to a sine wave, such that the minimum points won’t be right in the middle between the neighboring maximum points, and preferably with a parameter that would determine how close a minimum point is to the nearest maximum point.

I have found that the generalized Clausen function satisfies that requirement, but was wondering if anyone knows of a simpler function, which may be less computationally expensive. I need the function to be a single continuous function, and one that can be integrated, if possible.

Auggie
  • 155
  • 2
    Possible duplicate: https://math.stackexchange.com/questions/2430564/equation-of-a-tilted-sine/2430662 Here you can find many examples of "skewed" or "tilted" sine waves. – z100 Sep 09 '19 at 16:57
  • Thanks for that link! Glancing at the answers there, it seems like the simplest function would be y = sin(x + y/n). I am not sure how to integrate this type of function, but I’ll look into it. – Auggie Sep 09 '19 at 17:45

1 Answers1

0

How about shifting a parabola to the left and making it periodic? I.e., take $f$ where $$f(x)=\begin{cases} \hfil (x-a)^2 & \text{if $0 \leqslant x \leqslant 1$}\\ \hfil f(x-1) & \text{if $x>1$}\\ \hfil f(x+1) & \text{otherwise}? \end{cases}$$

If $a=\tfrac15$ you get

enter image description here

and $a=\frac13$ gets you

enter image description here

Do you require it to be continuous/differentiable or something?

Edit: The function I suggested is integrable but not continuous. If you want it continuous, we can take the slight modified version:

$$f(x) = \begin{cases} \frac{1}{a^2}(x-a)^2 & \text{if $0\leqslant x\leqslant a$}\\ \frac{1}{(a-1)^2}(x-a)^2 & \text{if $a\leqslant x \leqslant 1$}\\ f(x-1) & \text{if $x\geqslant 1$}\\ f(x+1) & \text{otherwise}. \end{cases}$$

where $0<a<1$. The illustration below shows what happens for different values of $a$.

enter image description here

Luke Collins
  • 8,838
  • Thank you for the answer! I was aiming for a single continuous function, and preferably one that can be integrated, if such function exists. I will edit the question to include that preference. – Auggie Sep 09 '19 at 17:21
  • The function I suggested in integrable, but not continuous. – Luke Collins Sep 09 '19 at 18:05
  • @Auggie I edited my answer to have a function which is both integrable and continuous. – Luke Collins Sep 09 '19 at 18:12
  • Thanks again! When I said a single continuous function, what I meant was not a piece-by-piece function (I am probably not using the correct terminology). I’m also confused as to how the function you suggested would generate periodicity. On the graphing calculator I’m using (Desmos) only the first two pieces return a graph, and it’s not periodic. – Auggie Sep 09 '19 at 23:32