1

For the inviscid Burgers' equation $$u_t + uu_x = 0,$$

with initial conditions (correct me if I am wrong, these are piecewise functions)

\begin{equation} u_a(x,0)=\left\{ \begin{array}{@{}ll@{}} -1, & \text{if}\ x<0 \\ +1, & \text{if}\ x\geq0 \\ \end{array}\right. \end{equation}

\begin{equation} u_b(x,0)=\left\{ \begin{array}{@{}ll@{}} +1, & \text{if}\ x<0\\ -1, & \text{if}\ x\geq0 \\ \end{array}\right. \end{equation}

I am trying to find their unique (entropy) solutions along with their breaking times. I would much prefer if you could explain your train of thoughts on how you obtained the solutions (accompanied by the solutions). Also, am I including the jump condition correctly? I have seen a few posts where the solutions include the speed itself within the conditions, e.g. this.

This looks very familiar with a lot of the Riemann examples I have seen on the site. Perhaps it may be a duplicate and I apologize for that. I have seen this where they discussed the non-convex case but I am not sure if it is applicable.

Here are the characteristic plots for both initial conditions.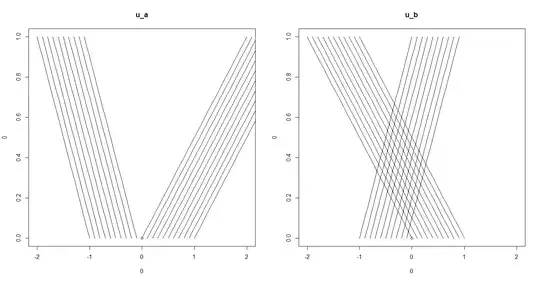

For $u_a$, we can observe that there is no intersection of the characteristic lines with solutions $u_L(x,t)=-1$ and $u_R(x,t)=1$ but there is an empty V-shaped region with no (classical) solutions. Furthermore, there is no breaking time since they do not intersect. How do I then proceed to find the weak solutions? Or to be more precise, how do you come up with other solutions? It seems to me from this post that since the flux function is convex, you can only create two types of solutions. I don't think a rarefaction is correct since there isn't a point where many characteristic lines are projecting out.

I am aware that a possible solution is

\begin{equation} u_a(x,t)=\left\{ \begin{array}{@{}ll@{}} -1, & \text{if}\ x<0 \\ +1, & \text{if}\ x\geq0 \\ \end{array}\right. \end{equation}

which satisfies the Rangine-Hugoniot jump condition, i.e. speed $s=\frac{(1/2-1/2)}{(-1-1)}=0$, and the condition is met where $(1/2-1/2)=s(-1-1)$ (both sides are $0$). Do we still say this has no breaking time? Furthermore, the (Lax) entropy condition requires $u^->s>u^+$ which is not met. Hence, this isn't an unique (entropy) solution.

For $u_b$, the lines intersect. The breaking times are computed as $\tau_B=-\frac{1}{u(x,0)_x}$, where $u(x,0)_x=\frac{\partial u(x,0)}{\partial x}=\infty$. Does that mean $\tau_B=0$ for $u_b(x,0)?$ (Did I perform the derivative incorrectly? I tried following a similar case from this post.)

In this case, is there even a solution?

PS: I realize there are a lot of minor questions contained here, I hope this is okay as I am trying to clear up my confusions on this topic in general.

mathnoob
  • 215
  • 2
    For $u_a$, the unique entropy solution would be to fill that empty V-shaped region with a "fan" of characteristics with speeds and values ranging from $-1$ to $1$. For $u_b$ your calculation of the breaking time is correct because immediately after you set this system in motion, the characteristics at $x=\pm \epsilon$ crash into each other. Characteristics can't really "intersect" (otherwise they aren't characteristics) so when they do run into each other, they form something called a shock, which is like a boundary line where characteristics from either side stops. – Ninad Munshi Aug 31 '19 at 21:15
  • I see. So for $u_b$, there is indeed no possible solution since a shock has occurred. Is there any other analysis that can be performed?

    Then for $u_a$, so it seems I was wrong and it indeed is a rarefaction? So I would have to use the shock speed to determine the solutions, which means the structure would look like $u(x,t)=-a,$ if $x<st)$.

     – mathnoob Aug 31 '19 at 21:34
  • 1
    For $u_b$ , even though there are infinitely many shocks possible, there is a max entropy shock, so it does have a unique solution. You just have to find the equation for the shock. For $u_a$ it is a rarefaction fan but using the shock speed equation is incorrect since it is not a shock. Instead draw out the characteristics and see if you can come up with a solution for the rarefaction characteristics and their values. – Ninad Munshi Aug 31 '19 at 21:38

1 Answers1

1

Let us follow the method in this post. We solve the Riemann problem of the inviscid Burgers conservation law $u_t + f(u)_x =0$, where the flux $f: u\mapsto \frac12 u^2$ is convex.

  • $u_a$. Here, characteristics separate. The entropy solution is the transsonic rarefaction wave $$ u_a(x,t) = \left\lbrace \begin{aligned} &{-1} && x\leq {-t}\\ &x/t && {-t}\leq x\leq t\\ &{+1} && {t}\leq x \end{aligned} \right. $$ The derivation of the waveform can be found e.g. in this post.

  • $u_b$. Here, characteristics intersect. The entropy solution is the shock wave $$ u_b(x,t) = \left\lbrace \begin{aligned} &{+1} && x< st\\ &{-1} && {st}< x \end{aligned} \right. $$ which speed $s=\frac12 (1-1) = 0$ is deduced from the Rankine-Hugoniot condition. Hence, this is a static shock.

These entropy solutions are valid for all $t>0$. The formula for the breaking time is valid for smooth initial data, where the solution keeps smooth until the classical solution's breakdown.

Note: the slopes of the characteristic lines in OP look incorrect. With the present initial data, these slopes should equal $u(x_0,0) = \pm 1$.

EditPiAf
  • 21,328
  • Regarding $u_a$,would it be more accurate if the intervals are $x<-t$, $-t \leq x <t$ and $x\geq t$? (where the empty region is $-t\leq \frac{x}{t} <t$) and yes, the slopes are inaccurate, I had a constant multiplied onto $u_R$ when I was experimenting. Thanks for pointing that out. – mathnoob Sep 01 '19 at 12:57
  • @mathnoob for the rarefaction, the solution is continuous for $t>0$. Thus, we can use $\leq, \geq$ for the inequalities – EditPiAf Sep 01 '19 at 15:24