Generalizing Archimedes' "The Quadrature of the Parabola"

Question

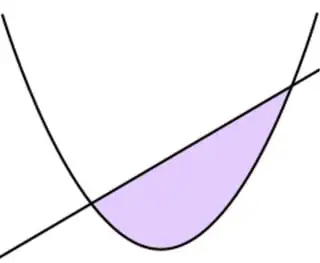
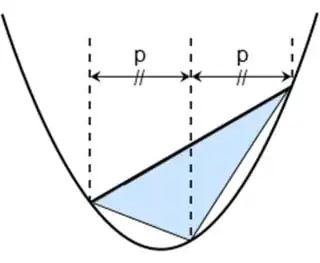
In the third century BC Archimedes discovered that

The area enclosed by a parabola and a line (left figure) is 4/3 that of a related inscribed triangle (right figure).

Consequentially, the area enclosed by a parabola and a line is 2/3 that of a parallelogram which has the chord and its tangential-to-the-parabola-copy as two of its sides. I have tried to derive this result myself using calculus.

Suppose $f:I \subseteq \mathbf{R} \to \mathbf{R}$ is a smooth convex function (so that the chord is on a fixed side of the graph), defined over some interval $I$. For $a < b$, let $[a,b] \subseteq I$ be a closed subinterval. The area of the segment bounded by the graph of $f$ and the chord $\overline{(a,f(a)) (b,f(b))}$ is given by $$\int_a^b \left( f(a)+(t-a) \frac{f(b)-f(a)}{b-a} - f(t) \right) \mathrm{d}t. \tag{1}$$ For the areas of the inscribed triangle and related parallelogram, we will use the point $c \in (a,b)$, which has the slope $$f'(c) =\frac{f(b)-f(a)}{b-a}.$$ Such a point exists according to the MVT, and it is unique because of the convexity of $f$. Thus $$c = c(a,b)= f'^{-1} \left( \frac{f(b)-f(a)}{b-a} \right). $$ The area of the aforementioned parallelogram is then the area between two parallel segments $$\int_a^b \left[ f(a)+(t-a) \frac{f(b)-f(a)}{b-a} - \left( f(c)+(t-c) \frac{f(b)-f(a)}{b-a} \right) \right] \mathrm{d}t.$$

Archimedes' result implies that

$$ \begin{align}&\int_a^b \left( f(a)+(t-a) \frac{f(b)-f(a)}{b-a} - f(t) \right) \mathrm{d}t \\ &= k \int_a^b \left[ f(a)+(t-a) \frac{f(b)-f(a)}{b-a} - \left( f(c)+(t-c) \frac{f(b)-f(a)}{b-a} \right) \right] \mathrm{d}t \end{align} \tag{3}$$

for $f(x)=x^2$, $a<b$, $c(a,b)=\frac{a+b}{2}$ and $k=\frac{2}{3}$.

My questions are about going in reverse:

1. Is it possible to systematically arrive at $f(x)=x^2$ (or a similar parabola), starting off with knowledge that $f$ is convex over some interval, $f$ satisfies Equation $(3)$ for all subintervals $[a,b]$ of its domain and $k=\frac{2}{3}$?
2. Is it possible to generalize this result by solving Equation $(3)$ for $k \neq \frac{2}{3}$ (clearly, $k \leq 1$)? I would appreciate guidance on how to do this if possible.

Thanks!

Answer 1

Let's rewrite $(3)$ with $a=x$, $b=x+h$ and consider $c$ as a function of $h$ (for a fixed $x$): $$ \tag{*} {h\over2}(f(x+h)+f(x))-\int_x^{x+h}f(t)\,dt= k\big[-h[f(c)-f(x)]+(c-x)[f(x+h)-f(x)]\big]. $$ We can differentiate both sides of $(*)$ with respect to $h$ a certain number of times (I'm supposing functions $f$ and $c$ are sufficiently regular), substituting then each time: $$ f'(c)= {f(x + h) - f(x)\over h},\quad c'(h)={h f'(x + h) - f(x + h) + f(x)\over h^2 f''(c)} $$ (the second equation can be obtained by differentiating the first one), and in the end take the limit of both sides for $h\to0$ (remembering that $c(0)=x$).

We obtain the first non-trivial equation after differentiating three times: I won't write down the intermediate result, which is quite long and complicated, but taking the limit $h\to0$ gives a simple result: $$ {1\over2}f''(x)=k{3\over4}f''(x), $$ which is satisfied either by $f''(x)=0$ (trivial solution: a straight line) or by $k=2/3$.

Hence it is not possible to solve equation (*) with $k\ne2/3$.

Substituting now $k=2/3$ into $(*)$ and differentiating five times with respect to $h$, as before, the limit for $h\to0$ gives this differential equation: $$ \tag{**} f^{(4)}(x)={5\over3}{\big(f^{(3)}(x)\big)^2\over f''(x)}. $$ This has the particular solution $f^{(3)}(x)=0$, which gives a parabola:

$$\tag{#} f(x)=\alpha x^2+\beta x+\gamma, $$

while the general solution is:

$$\tag{§} f(x) = \alpha \sqrt{x + \beta} + \gamma x + \delta, $$ where $\alpha$, $\beta$, $\gamma$, $\delta$ are arbitrary constants. But it is easy to see that the graph of $(§)$ is again an arc of a parabola, with equation: $(y-\gamma x-\delta)^2=\alpha^2(x + \beta)$.

Hence the parabola is the only non-straight curve obeying Archimedes' relation in the form given in the question as equation $(3)$. However, as a function, it can be written either in the form $(\text{#})$ or in the form $(§)$ given above.