An opening remark: The original PDE can actually be reduced to the heat equation by the substitution $u(x,t)=e^{-at} f(x,t)$. The observation that $a=\pi^2$ tends to produce $u(x,t)\to b\sin \pi x$ as $t\to \infty$ therefore amounts to the claim that $f(x,t)$ tends to behave like $e^{-\pi^2 t}\sin \pi x$ for large times. At one level, this is what we expect from the heat equation: If we fix the temperature at the endpoints of a rod to be $0$, then for large times the temperature in the rod will tend to zero as well.
However, this behavior cannot actually be true for all initial conditions. Returning to the original PDE, suppose $u(x,t)$ is some solution converging to $\sin \pi x$ as $t\to \infty$. Since both $u(x,t)$ and the steady state $\sin(\pi x)$ are solutions to a linear PDE, the function $u(x,t)-\sin(\pi x)$ is itself a solution to this same PDE. But this latter function converges to zero and so cannot display the desired convergence.
To understand these matters more systematically we analyze our PDE in terms of separation of variables, i.e, we look for solutions of the form $u(x,t)=X(x)T(t)$. This may be rearranged to obtain
$$\frac{T'(t)}{T(t)} =\frac{X''(x)}{X(x)}+a=\lambda$$ where $\lambda$ is the separation constant. To obtain nonzero solutions satisfying the Dirichlet boundary conditions, one may check that we must choose $\lambda=a-n^2 \pi^2$ and thereby obtain $X_n(x)=\sin(n \pi x)$. The time-dependent parts are then $T_n(t)=e^{(-n^2 \pi^2+a)t}.$ Hence the separation of variables solutions may be written as $$u_n(x,t) = e^{(a-n^2 \pi^2) t}\sin(n\pi x).$$ By forming linear combinations of these solutions, we obtain the ansatz
$$u(x,t) = \sum_{n=1}^\infty c_n e^{(a-n^2 \pi^2) t}\sin(n\pi x).$$
With this expression, the large-$t$ behavior becomes clear. If $a<\pi^2$, then every separable solution converges to zero at large times and so $u(x,t)\to\infty$ in this limit. If $a\geq \pi^2$, then the first harmonic will grow arbitrarily large with time and so $u(x,t)\to \infty$ as $t\to\infty$. However, if $a=\pi^2$, then every solution except $n=1$ converges to zero and we have $u(x,t)\to c_1 \sin(\pi x)$. (This is essentially the point made by Mark Fischler in comments.) The only way around this is if $c_1=0$, in which case the solution instead starts with the second harmonic $e^{(a-4\pi^2)t}\sin(2\pi x)$. As such, when $c_1=0,$ $c_2\neq 0$, and $a=4\pi^2$ we again expect convergence to the appropriate steady state, i.e., $u(x,t)\to c_2 \sin(2\pi x)$. Similar statements apply for $a=n^2\pi^2$.
P.S.: The knowledgeable reader may note two points that I have not discussed here. (1) How do I know that every solution to the PDE may be written as a sum of separable solutions? (2) Assuming my solution is of this form, how do I compute the coefficients $c_n$? But the answers to both queries are standard textbook material in Fourier series and so I will not address either here.
 But for $a>10$ the solution grows to infinity:
But for $a>10$ the solution grows to infinity: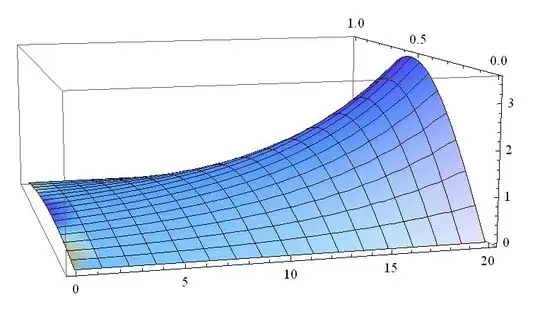 However, when I choose exactly $a=\pi^2$, every smooth initial condition I tried seems to give rise to a constant solution, here's for example $u_0(x)=-x^2+x$:
However, when I choose exactly $a=\pi^2$, every smooth initial condition I tried seems to give rise to a constant solution, here's for example $u_0(x)=-x^2+x$:
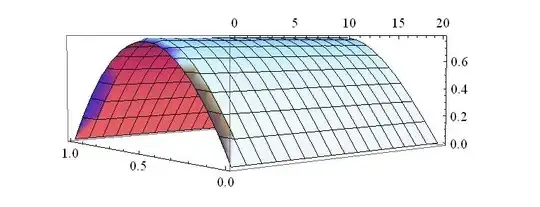 It gives the same result for all functions I tried like $u_0(x)=-3x^2+3x$ or $u_0(x)=\sin(\pi x)$.
It gives the same result for all functions I tried like $u_0(x)=-3x^2+3x$ or $u_0(x)=\sin(\pi x)$.