6

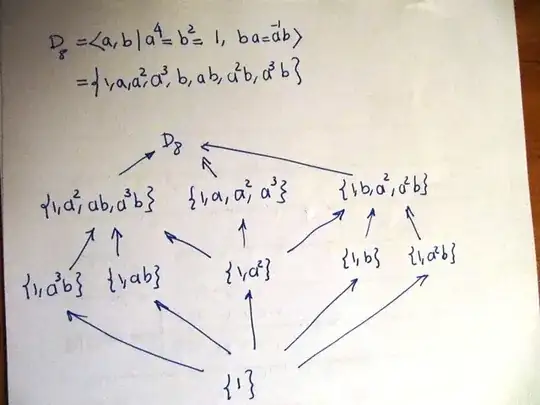
I am reading Fraleigh p. 80 in A First Course in Abstract Algebra, and in the book i see the elements and subgroup diagram of the dihedral group $D_4$. Here are they:

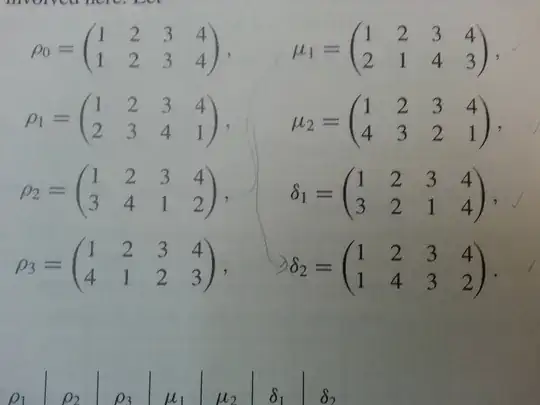
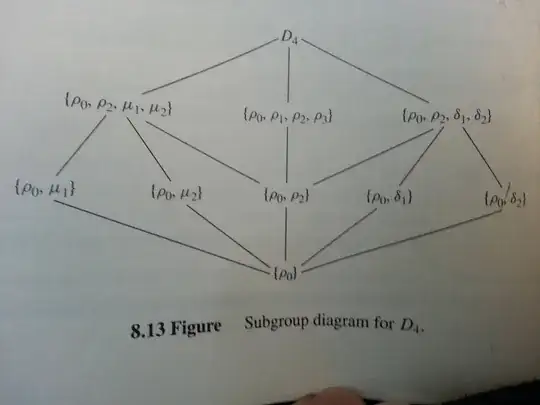
enter image description here

enter image description here

Here is how i try to draw the subgroup diagram: p0 must be included in every subgroup since it is identity element. Then i look at p1, and try to find the subgroups including p1, since p1 is included, the inverse of it must be included also, and p1op1 must be included also, and so on . I need to check whether the result of these computations make it closed. But this lookslike a very long process. Is there an easy way to do that? For example, by looking at u1 can we immediately say that it is included or not in a subgrouo without checking all compositions of u1 with u1? Or by looking at p1 can we find < p1 > easily? Thanks

Yasin Razlık
  • 1,805
  • 8
  • 30
  • 41
  • This is because either $u_1p_1$ or $p_1u_1$ is not in it, assuming $D_4=u_1,u_1^2,u_1^3.u_1^4,p_1,p_1u_1,p_1u_1^2,p_1u_1^3$ – NECing Mar 16 '13 at 14:13
  • yes, since it is not in the subgroup diagram i know it is not in it, but why? – Yasin Razlık Mar 16 '13 at 14:14
  • 1
    group has to be closed under operation – NECing Mar 16 '13 at 14:18
  • Thanks, but checking all possibilities looks like takes very long time. Is there any short way to understand whether a composition is an element of D4? – Yasin Razlık Mar 16 '13 at 14:26
  • There isn't many combinations. For instance, if $u_1$ is in it, then $\langle u_1\rangle$ is in it. – NECing Mar 16 '13 at 14:29
  • Yes, but it looks to me like finding ⟨u1⟩ takes a long time. Is there any way to find it easily? Do we need to calculate all these composition permutations? – Yasin Razlık Mar 16 '13 at 14:37
  • I tried ⟨u1⟩, ⟨u1⟩={p0, u1} and ⟨p2⟩={p0,p2}. But we see that {p0,p2,u1,u2} is also in it. So by checking ⟨a⟩, where a is in D4 we do not guarantee finding all subgroups? How do we find {p0,p2,u1,u2}? – Yasin Razlık Mar 16 '13 at 14:56
  • just find all elements of order 2, then find all elements of order 4. Then list they generate when you put them together. Sometimes you'll get a new group sometimes it's one you've already seen, but you'll quickly fill up that subgroup lattice if you do this. –  Mar 16 '13 at 14:59

2 Answers2

24

Personally, I am familiar to the following presentation of $D_4$ (or $D_8$). I added it here maybe you find it easier. In fact, You can feel the elements in this presentation easier. enter image description here

Mikasa
  • 67,942
0

Geometric interpretation is convenient for $D_4$. It is the invariance group of the square.

$D_4$ has three $\frac{\pi}{2}$ rotations, making up the subgroup $R_0$, $R_1$, $R_2$, $R_4$ (replacing $\rho$ of the textbook of the original query with upper case $R$). It is also clear that $R_0$ and $R_2$ ($\pi$ radians rotations) make up a subgroup.

$M_1$ and $M_2$ can be taken to be reflections in lines joining the opposite sides of the square and $d_1$ and $d_2$ are reflections in the two diagonals. It is obvious that each of these four elements squared is the identity, making four more proper subgroups of order 2.

A little visualisation shows that $R_2$ has the property of exchanging $M_1$ and $M_2$ and separately $d_1$ and $d_2$. This explains the other order 4 subgroups in the figure from the textbook.

Community
  • 1
Powstini
  • 1