$h(x)=\min\{f(x),\,g(x)\}$, it's possible that $\int_0^{\infty}h(x)\,dx<+\infty$? $\int_0^\infty f(x)\,dx,\;\int_0^\infty g(x)\,dx$ are divergent.

Question

Suppose $f(x),\,g(x)\in C([0,\,\infty))$ which are nonnegative and decreasing, such that $\displaystyle \int_0^\infty f(x)\,dx=\int_0^\infty g(x)\,dx=+\infty$. Let $h(x)=\min\{f(x),\,g(x)\}$, it's possible that $\displaystyle\int_0^{\infty}h(x)\,dx<+\infty$?

I just wander if there is an example? I can't find it.

Answer 1

Indeed such functions exist. We will consider 3 sequences $(x_n)$, $(y_n)$, $(\epsilon_n)$ of real numbers which will be useful for the construction. They are designed to satisfy the following conditions.

• $x_1 = 0$ and $x_n$ increases to $+\infty$ as $n\to\infty$.

• $y_n$ decreases to $0$ as $n\to\infty$.

• $\sum_{n \text{ odd}} (x_{n+1} - x_n) y_n = +\infty$ and $\sum_{n \text{ even}} (x_{n+1} - x_n) y_n = +\infty$.

• $\sum_{n\geq 1} (x_{n+1} - x_n) y_{n+1} < +\infty$.

• $0 < \epsilon_n < x_{n+1} - x_n$ and $\sum_{n\geq 1} \epsilon_n y_n < +\infty$.

If this seems too abstract, we may simply work with an example $x_n = n! - 1$, $y_n = \frac{1}{(n+2)!}$, and $\epsilon_n = \frac{1}{2}$. Next, we consider two functions $ u_n, l_n $ on $[x_n, x_{n+1}]$ so that

• the graph of $u_n$ is the linear interpolation of $(x_n, y_n), (x_{n+1} - \epsilon_n, y_n), (x_{n+1}, y_{n+1})$, and

• the graph of $l_n$ is the linear interpolation of $(x_n, y_n), (x_n + \epsilon_n, y_{n+1}), (x_{n+1}, y_{n+1})$.

$\hspace{7em}$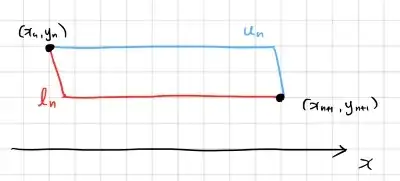

Finally, define

$$ f = [\text{concatenation of } u_1, l_2, u_3, l_4, \cdots ], \\ g = [\text{concatenation of } l_1, u_2, l_3, u_4, \cdots ]. $$

Then it is not hard to check that $f$ and $g$ satisfy the desired requirement, since

$$ \int_{0}^{\infty} f(x) \, \mathrm{d}x \geq \sum_{n\text{ odd}} \int_{x_n}^{x_{n+1}} u_n(x) \, \mathrm{d}x \geq \sum_{n\text{ odd}} (x_{n+1} - x_n - \epsilon_n) y_n = +\infty, \\ \int_{0}^{\infty} g(x) \, \mathrm{d}x \geq \sum_{n\text{ even}} \int_{x_n}^{x_{n+1}} u_n(x) \, \mathrm{d}x \geq \sum_{n\text{ even}} (x_{n+1} - x_n - \epsilon_n) y_n = +\infty \\ \int_{0}^{\infty} h(x) \, \mathrm{d}x = \sum_{n\geq 1} \int_{x_n}^{x_{n+1}} l_n(x) \, \mathrm{d}x \leq \sum_{n\geq 1} (x_{n+1} - x_n + \epsilon_n) y_{n+1} < +\infty.$$

Answer 2

If one removes the continuity condition at $x=0$, one could simply take $f(x)= \frac{1}{\sqrt{x}}$ and $g(x)= \frac{1}{x^{2}}$.