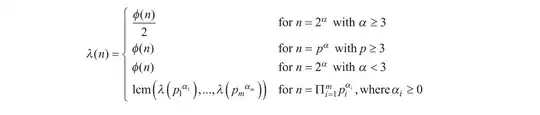Euler's totient theorem states that if $a$ and $n$ are coprime positive integers, then: $$a^{\varphi(n)} \equiv 1\;(\mathrm{mod}\;n)$$ So if $k$ is a given positive integer, which satisfies: $$\begin{cases} a^k \equiv 1\;(\mathrm{mod}\;n)\\ k\leqslant \varphi(n) \end{cases}$$
Does it necessarily hold that $k\,|\,\varphi(n)$?
No. For example $n=16$, $\phi(n)=8$, $a=9$, $k=6$. You can confirm that $$9^6\equiv1\pmod{16}\quad\hbox{but}\quad 6\not\mid8\ .$$
However if $a$ is given and $k$ is the smallest positive integer such that $a^k\equiv1\pmod n$, then it is true that $k\mid\phi(n)$. In the above example the smallest possible value of $k$ would have been $2$, not $6$.
No... This doesn't hold true if you take $n=16$ and $a=9$. You may easily check that $$9^6\equiv1\pmod{16}\quad\hbox{but}\quad 6\not\mid8\ .$$
Indeed, your assertion holds good if you are taking $k$ to be the order of $a$ in mod $n$. To find the minimum value of $k$, you should use an even stronger result which is Carmichael's Theorem; it states that the minimum value of $k$ is $\lambda(n)$ if $\gcd(a,n)=1$.
Note: Value of Carmichael Function does not depends on $a$ and obviously $\lambda(n)\mid \phi(n)$ .
No.
Say $n=15$. Then $\varphi (15)=8$. And $(4,15)=1$. But $4^{6}=(4^2)^3\cong1\pmod{15}$. And $6\not\mid8$.
Write $\varphi (n)=kq+r\,,r\lt k$. Then $1\cong a^{\varphi (n)}\cong a^r$. So if $k$ is the least such, then yes.
No ! But the only condition it is necessary for $a\notin [1]_n$ (where $[1]_n = \{x: x\equiv 1 \pmod{n}\}$ ) is that if $a^k \equiv 1 \pmod{n} $ then $\gcd(k , \varphi( n ))\neq1$
Proof. Assume $\gcd(k , \varphi( n ))=1$ then we with euclidean algorithm we got that $a^1 \equiv 1 \pmod{n} $ contradiction! $\square$
