Are these continued fractions of integrals known?

Question

_{Crossposted on MathOverflow}

Motivated by Bowman and McLaughlin (2000) on polynomial continued fractions, I considered an extension to functional continued fractions, where the numerator of each fraction is the integral of the previous fraction.

That is, define the continued fraction integral transform (CFIT) as \begin{align}\{\mathcal If(t)\}(s)=\dfrac{f(s)}{1+\dfrac{\int_0^s f(x)\,dx}{1+\dfrac{\int_0^s\int_0^u f(x)\,dx\,du}{1+\cdots}}}=\dfrac{f(s)}{1+\dfrac{f^{(-1)}(s)}{1+\dfrac{f^{(-2)}(s)}{1+\cdots}}}={\large{\mathop{\mathrm{K}}_{n=0}^{\infty}}}\frac{f^{(-n)}(s)}1\end{align} where $f\in C^\infty(\Bbb R)$ and $f^{(-k)}$ is Lagrange's notation for the $k$th antiderivative of $f$.

Some elementary properties of the transform include

$\{\mathcal I(0)\}(s)=0$;
$\{\mathcal If\}(0)=f(0)$;
$\{\mathcal If\}(s)=\dfrac{f'(s)}{\{\mathcal If'\}(s)}-1$ for all non-constant $f$ such that $f(0)=0$.

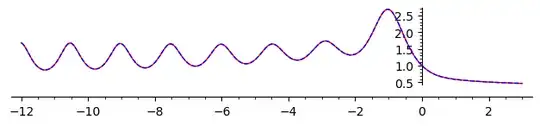
Considering the simplest, non-trivial case $f(t)\equiv1$, we have $f^{(-k)}(t)=t^k/k!$ so that $$\{\mathcal I(1)\}(s)=\dfrac{1}{1+\dfrac s{1+\dfrac{s^2/2!}{1+\cdots}}}.$$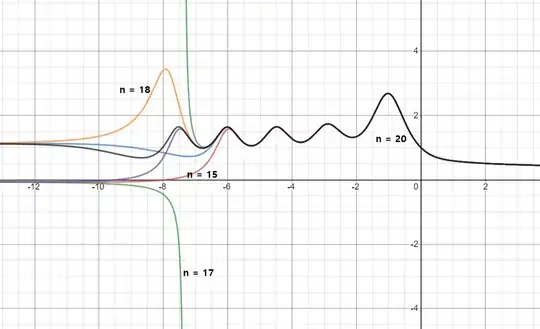

We can see that as $n$ increases, $\mathcal I(1)$ produces more waves. As @PeterForeman mentioned in the comments, the limit $\lim\limits_{s\to-\infty}\mathcal I(1)$ does not exist since it is zero for odd $n$ and $+1$ for even $n$. However, I believe there are more things that can be investigated.

Questions

Has the CFIT already been studied/discovered? If so, reference to literature would be appreciated.

Going back to the example of $\{\mathcal I(1)\}(s)$, is it true that the maximum value of each wave increases as $s$ increases up to the first wave? Are there an infinite number of such waves, and is there a closed form for $\max\mathcal I(1)$?

The period of the oscillations of $\mathcal I(1)$ appears to converge to $$\dfrac4e=1.4715\cdots$$ Can this be proven?

Empirically, the argmins are

-2.12897, -3.73409, -5.26940, -6.78494, -8.29119, -9.79168, -11.2881, -12.7814, -14.2723,
-15.7613, -17.2487, -18.7348, -20.2198, -21.7038, -23.1870, -24.6695, -26.1513, -27.6326,
-29.1133, -30.5937, -32.0736, -33.5531, -35.0323, -36.5111, -37.9897, -39.4680, -40.9461,
-42.4239, -43.9015, -45.3790, -46.8562, -48.3332, -49.8101, -51.2869, -52.7635, -54.2399,
-55.7162, -57.1924, -58.6685, -60.1445, -61.6203, -63.0961, -64.5717, -66.0473, -67.5228,
...

with consecutive differences

         1.60512, 1.53531, 1.51554, 1.50625, 1.50049, 1.49642, 1.49330, 1.49090, 
1.48900, 1.48740, 1.48610, 1.48500, 1.48400, 1.48320, 1.48250, 1.48180, 1.48130, 
1.48070, 1.48040, 1.47990, 1.47950, 1.47920, 1.47880, 1.47860, 1.47830, 1.47810, 
1.47780, 1.47760, 1.47750, 1.47720, 1.47700, 1.47690, 1.47680, 1.47660, 1.47640, 
1.47630, 1.47620, 1.47610, 1.47600, 1.47580, 1.47580, 1.47560, 1.47560, 1.47550, ...

@TheSimpliFire Also $\lim_{s\to-\infty}I(1)$ clearly does not exist as it equals $0$ for any odd number of terms in an approximation and $1$ for any even number. — Peter Foreman, Jul 06 '19 at 20:16
For $3.$, does one need $f(0) = 0$ since $\int_0^s f'(x) dx = f(x) - f(0)$? — Stephen Harrison, Jun 01 '23 at 06:15
@StephenHarrison Correct, edited. This would perfectly align with the previous property, substituting $s=0$ and using $2.$ gives $f(0)=\frac{f'(0)}{f'(0)}-1$. — TheSimpliFire, Jun 01 '23 at 20:31
It isn't completely clear to me why taking $\lim_{s \rightarrow -\infty} \sum_{k=0}^N$ for $N$ even/odd implies the limit doesn't exist for $N= \infty$. It seems like commutation of limits. — Stephen Harrison, Jun 02 '23 at 21:36

score 5 · Answer 1 · edited Jul 29 '22 at 00:20

Not an answer, but one more picture, with the functions for 100 and 150 terms superposed.

It is not clear what is happening on the left.

EDIT:

Here is the code (using sagemath):

def fun(x, N=150):
    L = [x**k/gamma(k + 1) for k in range(N, -1, -1)]
    resu = 1.0
    for t in L:
        resu = t / (1 + resu)
    return resu
P1 = plot(lambda x:fun(x, 100),-12, 3, aspect_ratio=1, color='red'); P1

score 2 · Answer 2 · answered Jun 06 '23 at 01:47

For your question:

Has the CFIT already been studied/discovered? If so, reference to literature would be appreciated.

I am not sure, but surprisingly, your example of $\{\mathcal I(1)\}(s)$ appears in the entry of OEIS sequence A319173

Expansion of e.g.f. 1/(1 + x/(1 + (x^2/2!)/(1 + (x^3/3!)/(1 + (x^4/4!)/(1 + ...))))), a continued fraction

This sequence was authored on Sep 12, 2018 by Ilya Gutkovskiy. Unfortunately, there is no other relevant information there yet.

Are these continued fractions of integrals known?

2 Answers2