Grazing area for a goat around a circle.

Question

I am doing this math question and i am really confused on how to approach it.

This is the question:

A retired mathematics professor has decided to raise a goat. He owns a silo and a barn. The barns front wall is tangent to the silo at the corner. The silo has a circular base with a radius of 10 feet. The professor has decided to tether the goat to a chain that is anchored at the corner of the barn, the point of tangency. He has also cut the chain so that it is long enough to wrap around the silo exactly once- that is, the length of the chain equals the circumference of the silo. The barn length is longer than the chain.

This is an image of the barn (square), the silo (circle) and the goat's grazing area.

The answer I got is -4762.48876, but area is positive, so i made it 4762.48876.

These are the steps i took to getting the answer I have:

$$x(\phi)= -R\sin\phi + \phi R\cos\phi, \qquad y(\phi) = R-R\cos\phi - \phi R\sin\phi$$

Answer 1

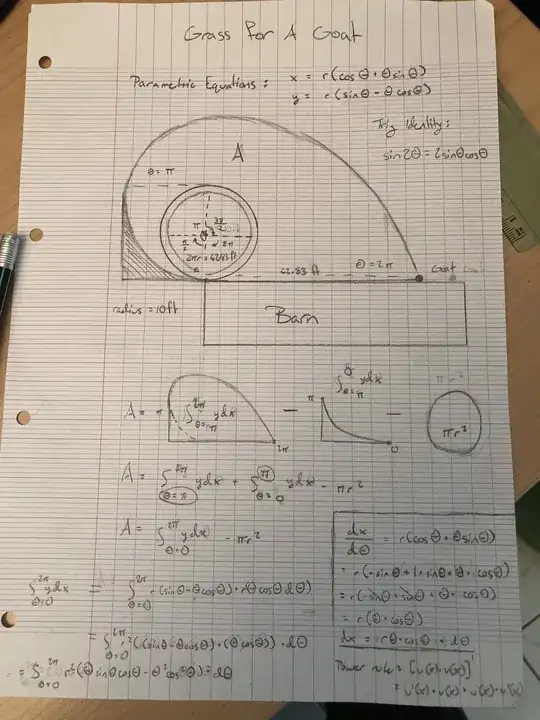
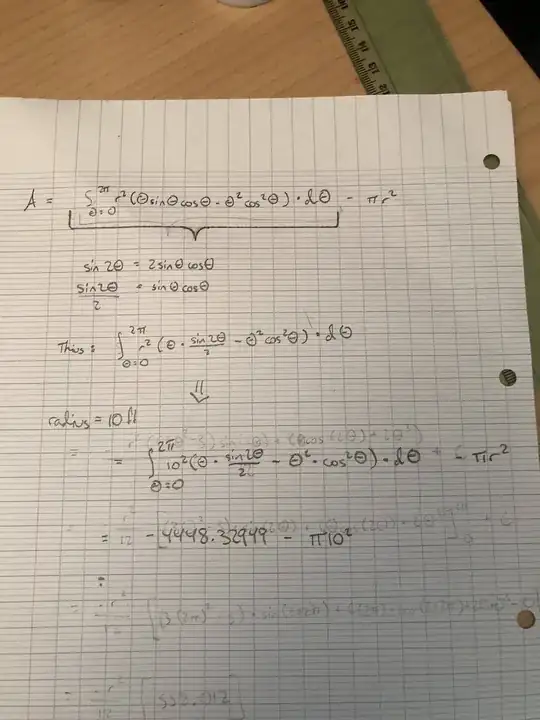From what I can see from the parametrization you've written, you have axis $x$ directed down, and axis $y$ directed left, is that right? That means you have the axes oriented in a way opposite than it's normaly done ($y$ counterclockwise to $x$). This is the origin of your opposite sign.

I suggest using axis $x$ oriented right and axis $y$ oriented up, as that's how they are usually drawn, so it's harder to make a mistake. The center of the coordinate system will be the center of the base of the silo.

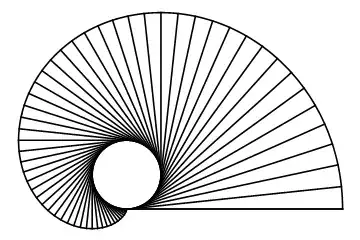
You can paramterize the border of the grazing area by $$ x(\phi)= -R\sin\phi + \phi R\cos\phi, \qquad y(\phi) = -R\cos\phi - \phi R\sin\phi$$ where $R=10 {\rm m}$ and $\phi$ is the angle showing how much of the chain is unwinded and does not follow the circumference of the silo. We have $\phi\in[0,2\pi]$.

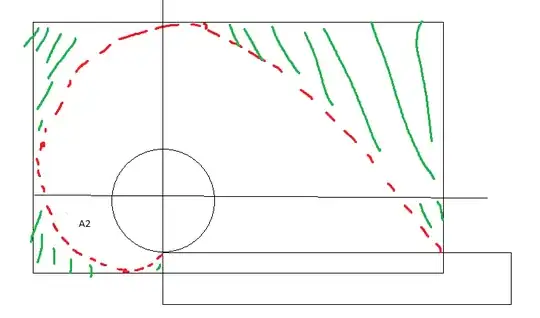
We can note that for $x$ initially decreases from $0$ for $\phi=0$ to some $x_{\rm min}<0$ for some $\phi=\phi_0$ (as it will turn out, the value of $\phi_0$ is not important) before it starts icreasing and reaches $x=2\pi R$ for $\phi=2\pi$. For $x<0$ we have two possible values of $y$ one related to $\phi<\phi_0$ and the other from $\phi>\phi_0$. Let's denote them $y_1(x)$ and $y_2(x)$. For $x>0$ we have only $y_2(x)$, but the lower boundary of this region is the wall for $y=-R$.

The full area surrounded by the chain, including the base of the silo, is given by \begin{align} S &= \int_{x_{min}}^0 (y_2(x)-y_1(x))dx + \int_0^{2\pi R} (y_2(x)-(-R)) dx =\\ &= - \int_{x_{min}}^0 y_1(x) dx + \int_{x_{min}}^{2\pi R} y_2(x) dx + 2\pi R^2=^\text{changing variables} \\ &= - \int_{\phi_0}^0 y(\phi) \frac{dx}{d\phi}(\phi) d\phi + \int_{\phi_0}^{2\pi} y(\phi) \frac{dx}{d\phi}(\phi) d\phi + 2\pi R^2= \\ &= \int_0^{\phi_0} y(\phi) \frac{dx}{d\phi}(\phi) d\phi + \int_{\phi_0}^{2\pi} y(\phi) \frac{dx}{d\phi}(\phi) d\phi + 2\pi R^2= \\ &= \int_0^{2\pi} y(\phi) \frac{dx}{d\phi}(\phi) d\phi + 2\pi R^2 = \\ &= (-\pi + \frac43\pi^3)R^2 + 2\pi R^2 = \\ &= (\pi + \frac43\pi^3)R^2 \end{align}

At the end we need to subtract $\pi R^2$, which is the area of the silo's base to get the answer: $$ A = \frac43 \pi^3 R^2 \approx 4134 {\rm m}^2$$

Answer 2

I have found another, much simpler derivation of the result. Let us divide the area of grazing into infinitesimaly thin triangles, as below:

They all approximately isoceles. The triangle with the apex at point $(R\sin\phi,R-R\cos\phi)$ has the legs of the length $L(\phi) = (2\pi-\phi)R$ (the length of unwinded chain). they are supposed to be very thin, with the angle at the apex being $\Delta\phi$. Therefore, the area of each triangle is

$$\Delta S \approx \frac12 L(\phi)^2 \sin( \Delta\phi) \approx \frac12 (2\pi-\phi)^2R^2 \Delta\phi$$

The full area is therefore equal to

$$ S = \int_0^{2\pi} \frac12 (2\pi-\phi)^2 R^2d\phi = -\frac{(2\pi-\phi)^3R^2}{6}\Big|_{\phi=0}^{2\pi} = \frac43\pi^3R^2$$

The previous method I've given is more general: it can be used for any area with a boundery with known parametrization. This answer is specific to this problem.