Nomogram for $z = x + \sqrt{x-y}$

Question

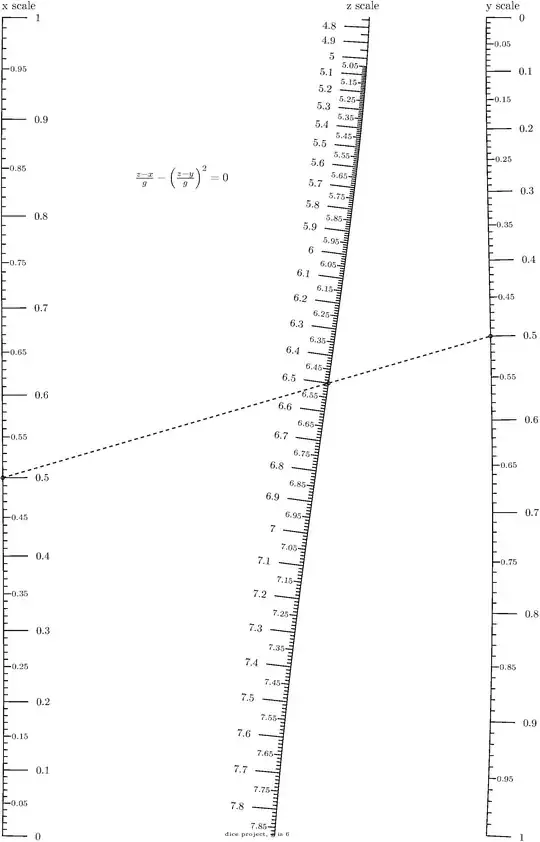
I am attempting to make a nomogram for the equation

$$\frac{z-x}{g} - \left(\frac{z-y}{g}\right)^2 =0$$

(here $g$ is a constant). You can use the quadratic formula to solve for $z$, in which case:

$$z = \frac{g}{2} + y \,\pm \, \sqrt{g}\sqrt{\frac{g}{4} + y-x}$$

And we can take just the positive branch, for example. What stumps me is the presence of $y-x$ under the square root, along with $y$ being outside of the square root. It seems difficult to find a way to separate the $y-x$ term to form a determinant.

I can of course reparameterize with $c\equiv y-x$ so that $$z=\frac{g}{2} +x+c \pm\;\sqrt{g}\sqrt{\frac{g}{4} + c}$$

but reparameterization is inconvenient for my application (computing outcomes when rolling dice).

I have also considered moving the $y$ term to the left hand side and squaring, but this creates a lot of linearly-independent terms:

$$z^2 - 2(y-g/2)z + (y-g/2)^2 = g(x-y) + g^2/4$$

Substituting $u\equiv (x - g/4)$ and $v \equiv (y-g/2)$, we have the slightly simpler form:

$$(z-v)^2 = g(u-v)$$

$$z^2 - 2vz + v^2 = g(u-v)$$

There are three variables and five functional forms $z^2, z, v, v^2, u$, making this apparently a nomogram of genus 5-3 = 2.

Is there a way forward?

Answer 1

It can't be done directly.

1. According to Warmus's procedure, you can compute the rank of your equation $F(x,y,z) = \frac{z-x}{g} - \left(\frac{z-y}{g}\right)^2 = 0$ with respect to each of the three variables $x$, $y$, and $z$. The ranks are 2, 3, 3, respectively, because we can decompose them in the following way:

   • $F(x,y,z) = x\cdot\color{gray}{(\ldots)} + 1\cdot\color{gray}{(\ldots)}$
   • $F(x,y,z) = y^2\cdot\color{gray}{(\ldots)} + y\cdot\color{gray}{(\ldots)} + 1\cdot\color{gray}{(\ldots)}$
   • $F(x,y,z) = z^2\cdot\color{gray}{(\ldots)} + z\cdot\color{gray}{(\ldots)} + 1\cdot\color{gray}{(\ldots)}$

   where the factors on the left are linearly independent functions of the one variable, and the terms in parentheses are functions of the other two variables only.

   These ranks [2,3,3] are valid—they don't rule out the possibility of a nomogram. So we must test further.

2. Write $F(x,y,z) = x\cdot G_1(y,z) + 1\cdot G_2(y,z)$. Here, $G_1(y,z) \equiv -1/g$ and $G_2(y,z) \equiv \frac{z}{g}-\left(\frac{z-y}{g}\right)^2$. Unfortunately, if we compute the rank of $G_2$, we find that it is rank 3: $$G_2(y,z) = z^2\color{gray}{(\ldots)} + z\color{gray}{(\ldots)} + 1\color{gray}{(\ldots)}.$$

3. Unfortunately, the ranks of $G_2$ and $G_3$ must be 1 or 2 in order for the original function $F$ to be nomogrammable directly. Hence your function $F(x,y,z)$ is not nomogrammable directly.

4. "Nomogrammable directly" means that you can write $F(x,y,z)$ as the determinant of a matrix in Massau normal form (a 3x3 matrix where each row is a function of a single variable).

   It is still possible in theory that you could find a strictly positive function $G(x,y,z)$ such that $F(x,y,z)G(x,y,z)$ is nomogrammable. This function would have the same zeroes as $F(x,y,z)$ and so a nomogram for this function would be usable as a nomogram for $F$. The only difference is that in a direct nomogram, if you mark a point on each of the three axes, the area of the resulting triangle corresponds to the value of $F$, whatever it is. In contrast, for this kind of indirect nomogram, the area of the triangle is meaningless; you only have the alignment property, which is that you can find the zeroes of the function by finding where points on each of the three scales lie on a line (on a triangle of zero area).

Answer 2

You could try a numerical solution. Pynomo contains a module called nomogen that can do that.

You didn't say what range your variables cover, I assumed x & y are probabilities and set g to 6.

This produces a solution, I have posted the results and python code here.

Here is a jpg of the nomogram