I am trying to understand why polynomial long division algorithm works. I have found an answer on Quora, please follow the link: Why does polynomial long division work?
As you can see the explanation comes along with the example:
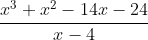
And the first step is calculation of the division of the leading terms of numerator and denominator and getting to know how much this differs from the original fraction. In this case: 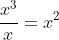
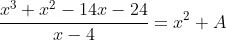
What I can not understand is why we can perform this first step(why we can divide only leading terms of every polynomial). Could you please explain.
Thanks in advance.