Law of large numbers for dependent random variables with fixed covariance

Question

Given identically distributed random variables $X_1,...,X_n$, where $ \mathbb E X_i = 0$, $\mathbb E [X_i^2] = 1$, and $\mathbb E [X_i X_j] = c<1$, define $S_n = X_1 + ... + X_n$. Will

$$\frac{S_n}{n} \rightarrow 0$$ in probability as $n\rightarrow \infty$?

The closest question I could find is this one, where an additional constraint is placed on the covariances, such that Chebyshev inequality can be used to bound $\left|\frac{S_n}{n} \right|$ by $\text{Var}\left(\frac{S_n}{n}\right)$. However, in my case $\text{Var}\left(\frac{S_n}{n}\right)$ is constant, so this approach will not work.

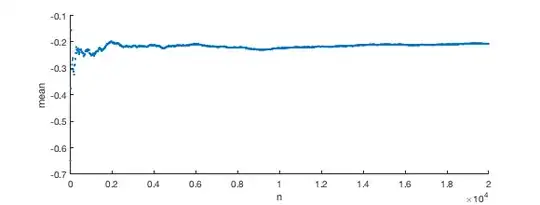
Indeed, when I simulate using MATLAB on an example where I generate Gaussian random variables which all have covariance $c=0.1$, I do not see it approaching zero.

rng(1)
NN =20000;
C = ones(NN,NN)*0.1 + 0.9*diag(ones(NN,1));
rndnums = mvnrnd(zeros(NN,1), C, 1);
NNs = 1:20:NN
means = -99*ones(1,length(NNs));
for ti=1:length(NNs)
    means(ti) = mean(rndnums(1,1:NNs(ti)));
end
scatter(NNs ,means, '.'); xlabel('n'); ylabel('mean')

Intuitively, since all the variables are all "locked" to eachother in correlation, I can't imagine how their mean will "eventually" reach zero.

Is there a law of large numbers in this context? If so, what is the rate of convergence? Or if not, is there any way to tell what it will converge to?

Answer 1

Letting $A$ be the ($n\times n$) matrix with ones in all entries, and $I$ be the $n\times n$ identity matrix, the covariance matrix is $$ M = (1-c)I + cA = P D P^{-1} $$ where $D$ is diagonal and $P$ is orthogonal, and (as @RobertIsrael observed) we are free to order the eigenvalues such that the upper left element of $D$ is $1+(n-1)c$ and the remaining diagonal elements are $1-c$.

When we do this, we find that $(1,1,1,\ldots,1) P = (\sqrt{n},0,0,0...)$ which tells us that the linear combinations of the variates that do not constitute the eigenvector with eigenvalue $(1-c)$ do not contribute to the sum $S_n$.

So the sum $S_n$ is distributed as $\sqrt{n}$ times a variate with mean zero (of course) and variance $1+(n-1)c$. This need not be a Gaussian but if the tails are not thick (so that the law of large numbers applies) then for large $n$ the standard deviation of $S_n/n$ goes like $$ \frac{\sqrt{n}\sqrt{1+(n-1)c}}{n} \sim \sqrt{c} $$ So $S_n/n$ will not approach zero with probability one.

I think even if the individual variates have thick tails, that only makes matters worse for saying that $S_n/n$ will approach zero with probability one, so the above statement still holds.