Weighting a cubic hermite spline

Question

I am trying to figure out a function behind the software's curve drawing algorithm. Originally, each node comes with 3 parameters : time, value, and tangent. I have found that it fits cubic Hermite spline, and confirmed that using the equation from the Wikipedia gives me equal result to the software's evaluation.

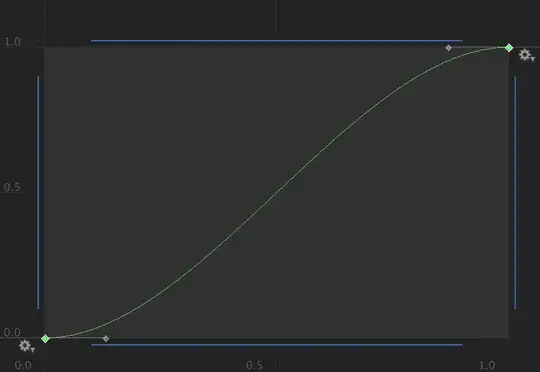
The following curve is when both tangents are 0.

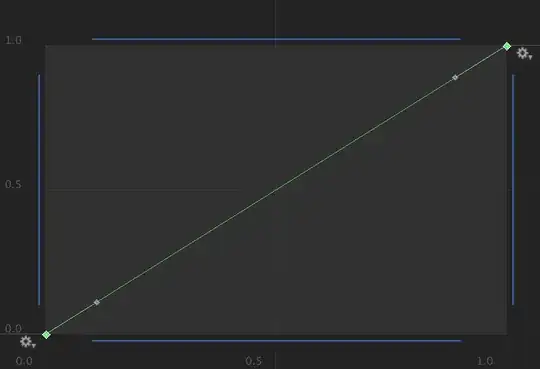
The following curve is when both tangents are 1 (45 degree).

But this software has "weight" value on each node, which ranges from 0 to 1. I am trying to figure out how the weight could affect the spline empirically. Here's my observation :

The weight ranges from 0 to 1. In this gif below, dragging the handle to the right increase the weight. Dragging stretch up do not affect the weight (however you are changing the tangent)

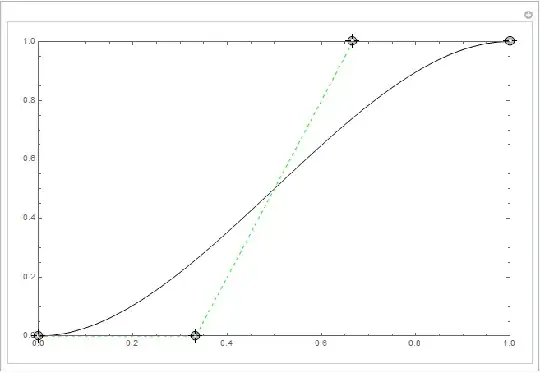
When both tangents are 0, with weight applied and both weight are 0.3333333, it results in the same shape as if no weights are applied. (The smooth S shape, the first image) I think this is the biggest hint, 0.3333333 may has to do something with the "cubic" function. Below is an image of this.

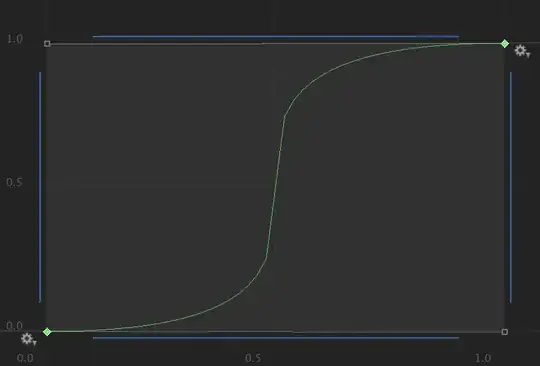
When both tangents are 0, with weight applied and both weight are at maximum 1, the curve skewed further in X axis to meet at the center between 2 points. Indicating that, weight 1 doesn't mean unweighted like a weight function would have behave but rather really maximum possible weight. Below is an image of this.

When both tangents are 0, with weight applied and both weight are 0, results in a linear graph as if their tangents are 1. Below is an image of this.

When both tangents are 1, weight do not affect their shape at all no matter the value. It stays linear. Suggesting that weight do something to the components which became tangent, but nullified when both components are equal. I guess it did something to the cos component? Since with maximum weight the graph skewed further in X axis.

However if the other tangent is not 1, changing the weight of the side that has tangent 1 do affect the shape. Indicating that the weight is not simply "weighting that side's tangent".

If someone could figure out where the weight should be applied (or any example spline you know with weight parameter), it is very much appreciated. Thank you.

Answer 1

It's a Bézier curve. (No, Unity does not have a copyright or patent on Bézier curves.) Cubic Bézier curves are widely used in the computer graphics industry to create smooth curves like this one. You give the two endpoints of the curve $P_0, P_3$ and two intermediate "control points" $P_1,P_2$ and it produces a smooth curve that is tangent to the line $P_0P_1$ at the start and $P_2P_3$ at the end, where the magnitude of the derivative at these points is proportional to the distance $|P_0-P_1|$ and $|P_2-P_3|$.

$$x(t)=(1-t)^3x_0+3(1-t)^2tx_1+3(1-t)t^2x_2+t^3x_3$$ $$y(t)=(1-t)^3y_0+3(1-t)^2ty_1+3(1-t)t^2y_2+t^3y_3$$

In this case, $P_0=(0,0)$ and $P_3=(1,1)$, and you are adjusting the locations of the control points $(x_1,y_1)$ and $(x_2,y_2)$. The "weights" are the values $x_1$ and $1-x_2$.

One thing which makes the Unity graph a bit interesting is that it's been re-parameterized as a function $y(x)$, by inverting $x(t)$ and plugging in to $y(t)$, so it's not a simple cubic anymore in its expression (hence why the derivative goes to infinity in the limiting example). The function $x(t)$ stops being injective if you make the weights larger than 1, which is why that's the upper limit.

When $x_1=1/3$ and $x_2=2/3$ then $x(t)=t$, so $y(x)$ is just a cubic function. This is the "unweighted" case. (Note that in the unity interface the handles have a fixed length in "unweighted" mode, so the locations of the handles is not the location of the control points which threw me off a bit. To find the location of the control point, extend the line from the handle until it meets the line $x=1/3$.) When you turn on "weighted" mode, the handles are actually on the control points.

Here's a Mathematica script that you can play with to see how moving the control points affects the curve, along with pictures for the "default" and "extreme" cases:

Manipulate[Graphics[{BezierCurve[pts, SplineDegree -> 3], Dashed, Green, Line[pts]},
  PlotRange -> {{0, 1}, {0, 1}}, Frame -> True, AspectRatio -> 1/1.6, ImageSize -> 600],
 {{pts, {{0, 0}, {1/3, 0}, {2/3, 1}, {1, 1}}}, Locator, LocatorAutoCreate -> True}]

Answer 2

Here's a solution in C# which I believe duplicates the function of the Unity AnimationCurve according to the answer by @Mario Carneiro.

I've used doubles instead of floats for reasons particular to my own need to solve this problem. The value of Eps would need to be changed to the corresponding Machine Epsilon for floats. It might be useful to also have a check for excessive iterations and throw to avoid infinite loops.

I have a check which short circuits the rootfinding problem to solve the cubic hermite problem, which depends specifically on the weights matching the floating point value 1/3.0 precisely, which integrates with the rest of my API, one might consider checking for equality to machine precision there. Also if anyone uses the floating point code directly, be careful of converting from 1/3.0f to 1/3.0d if converting from unity AnimationCurves in order to have the short circuit work correctly.

Using Halley's method over Newton-Raphson gave a significant speedup, using the third order Householder method gave another ~10% boost. Cardano's method of solving the cubic equation is probably slower due to the need to do several square/cube roots which would all be iterative methods.

For some reason it performs faster with doubles than floats for me(!) and is comparable to the Unity AnimationCurve performance (presumably done in C++).

I thought about a short circuit for when the problem fits a quadratic exactly, but that is probably unlikely to be hit as an actual use case.

    public const double Eps = 2.22e-16;
public static double AnimationCurveInterpolant(double x1, double y1, double yp1, double wt1, double x2, double y2, double yp2, double wt2, double x)
{
    double dx = x2 - x1;
    x = (x - x1) / dx;
    double dy = y2 - y1;
    yp1 = yp1 * dx / dy;
    yp2 = yp2 * dx / dy;
    double wt2s = 1 - wt2;

    double t = 0.5;
    double t2;

    if (wt1 == 1 / 3.0 && wt2 == 1 / 3.0)
    {
        t  = x;
        t2 = 1 - t;
    }
    else
    {
        while (true)
        {
            t2 = (1 - t);
            double fg = 3 * t2 * t2 * t * wt1 + 3 * t2 * t * t * wt2s + t * t * t - x;
            if (Math.Abs(fg) < 2*Eps)
                break;

            // third order householder method
            double fpg = 3 * t2 * t2 * wt1 + 6 * t2 * t * (wt2s - wt1) + 3 * t * t * (1 - wt2s);
            double fppg = 6 * t2 * (wt2s - 2 * wt1) + 6 * t * (1 - 2 * wt2s + wt1);
            double fpppg = 18 * wt1 - 18 * wt2s + 6;

            t -= (6 * fg * fpg * fpg - 3 * fg * fg * fppg) / (6 * fpg * fpg * fpg - 6 * fg * fpg * fppg + fg * fg * fpppg);
        }
    }

    double y = 3 * t2 * t2 * t * wt1 * yp1 + 3 * t2 * t * t * (1 - wt2 * yp2) + t * t * t;

    return y * dy + y1;
}