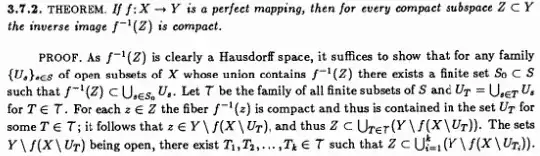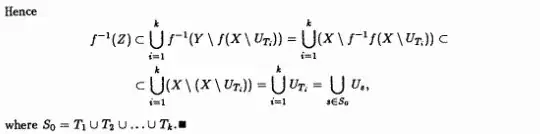17

I'm trying to solve the following exercise of the book "Grupos de Lie - Luiz A. B. San Martin (exercise 18, page 55)":

Exercise: Let $G$ be a topological group (if necessary, $G$ is Hausdorff) and $H_1 \subset H_2\subset G$ closed subgroups of $G$. Show that if $G/H_2$ and $H_2/H_1$ are compact, then $G/H_1$ is compact.

Some comments...

It is easy to see that the function \begin{align*} \pi: G/H_1 &\to G/H_2 \\ g H_1 & \mapsto g H_2, \end{align*} is a continuous and open function, nevertheless $\pi$ also satisfies $g_1 \cdot \pi(g_2) = \pi(g_1\cdot g_2)$, $\forall \ g_1 \in G,\ $ ($g_1 \cdot (g_2 H) = (g_1 \cdot g_2) H$).

Although I am aware of the following theorem:

Theorem: Let $G$ be a topological group, and $H$ a closed subgroup of $G$, if $H$ and $G/H$ are compact then $G$ is compact.

I can't apply it to solve my problem, once neither $G/H_1$ nor $H_2/H_1$ are topological groups.

So, I tried to adapt the proof of the theorem cited above for my case, and it is necessary to show that the function $ \pi $ is a closed function, which I was not able to conclude.

Can anyone help me?

Matheus Manzatto
  • 3,271
  • Why wouldn't $G / H_1$ and $G / H_2$ be topological groups? – Mark Kamsma Apr 23 '19 at 21:45
  • $H_1$ and $H_2$ are not normal subgroups. – Matheus Manzatto Apr 23 '19 at 21:46
  • Ah yes, I was focusing on the topological bit. In your definition of a topological group, are they always Hausdorff? – Mark Kamsma Apr 23 '19 at 22:28
  • Unfortunately not. – Matheus Manzatto Apr 23 '19 at 22:29
  • You don't need the requirement that $G/H$ is a (topological) group to prove the quoted theorem. For example, see If and / are compact, then is compact.. $G/H$ is always well-defined (though may not be a group) provided that $H$ is a subgroup of $G$ – YuiTo Cheng Apr 24 '19 at 02:09
  • @YuiToCheng but to "use" (I don't know a good word to express what I want) this proof, we need to prove that $\pi$ is a closed function. I don't know how to show this. – Matheus Manzatto Apr 24 '19 at 02:13
  • @MatheusManzatto quotient map is always closed as long as $H$ is compact, see Henno Brandsma's answer. In your case, notice $G/H_2$ is isomorphic to $(G/H_1)/(H_2/H_1)$ – YuiTo Cheng Apr 24 '19 at 02:15
  • isomorphic --> natural bijection (as they are not necessarily groups). In fact, the natural bijection is exactly the same as the one in the third isomorphism theorem – YuiTo Cheng Apr 24 '19 at 02:21
  • @YuiToCheng In the answer that you linked, Henno says that the projection $p: G \to G/H$ is closed because $p^{-1} ( g H) $ is compact for every $g H \in G/H$. Do you know why this is true? I generally prove that $p$ is closed in the following way, if $F \subset G$ is closed then $p^{-1}(p(F)) = FH$, once $F$ is closed then $H$ and compact, then $FH$ is closed $\Rightarrow$ $p$ is closed. – Matheus Manzatto Apr 24 '19 at 02:28
  • Your proof is correct. – YuiTo Cheng Apr 24 '19 at 02:29
  • I just want to fix something that I said wrong in the above comment, Henno never said "$p:G→G/H$ is closed because $p^{−1}(gH)$ is compact for every $gH∈G/H$". He just reiterated something that the OP said in the question. Probably, the OP has demonstrated such result in the same way that I described above (since it is a standard demonstration). The problem of this method is that, at first, we cannot adapt this proof for the case described in my question, once there is not a product defined in $G/H_1$. – Matheus Manzatto Apr 24 '19 at 03:42
  • 1
    I'm now suspecting the statement is actually false. (without the normality assumptions) – YuiTo Cheng Apr 26 '19 at 15:43
  • Me too. But I swear I copied the exercise exactly as it is in the book. – Matheus Manzatto Apr 26 '19 at 16:06

1 Answers1

7

Lemma. The map $\pi$ is closed.

Proof. Let $F_1\subset G/H_1$ be any closed set and $x_2\in G/H_2\setminus \pi(F_1)$ be any point. We shall construct a neighborhood of $x_2$ disjoint from $\pi(F_1)$. For each $i=1,2$ let $q_i:G\to G/H_i$ be the quotient maps. We have $q_2^{-1}(x_2)=xH_2$ for some point $x\in G$. Put $F=q_1^{-1}(F_1)$ and remark that $F$ is closed in $G$ and $F=FH_1$. Since $x_2\not\in \pi(F_1)$, the sets $F$ and $xH_2$ are disjoint. Let $y\in xH_2$ be any point. Since the set $F$ is closed, $y\not\in F$, and $G$ is a Hausdorff topological group, there exists an open neighborhood $O_y=O_y^{-1}$ of the identity of $G$ such that $O_y^2y\cap F=\varnothing$. Since $F=FH_1$, $O_y^2yH_1\cap F=\varnothing$ and so $q_1(O_y^2yH_1)\cap q_1(F)=\varnothing$. Remark that $O_{y1}=q_1(O_yyH_1)$ is an open neighborhood of a point $yH_1\in G/H_1$. Since a map $tH_1\mapsto xtH_1$ for each $t\in H$ is a homeomorphism of a space $G/H_1$, the set $xH_2/H_1$ is homeomorphic to $H_2/H_1$, so it is compact. Since $\{O_{y1}:y\in xH_2\}$ is an open cover of the set $H_2/H_1$, there exists a finite subset $Y$ of $xH_2$ such that $xH_2\subset\bigcup \{O_{y1}:y\in Y\}$. Put $O=\bigcap\{Oy: y\in Y\}$. We claim that $F\cap OxH_2=\varnothing$. Indeed, suppose to the contrary that there exists a point $z\in F\cap OxH_2$. Since $xH_2\subset\bigcup \{O_{y1}:y\in Y\}$, there exists a point $y\in Y$ such that $z\in O=O_yyH_1\subset O_y^2H_1$, a contradiction, because $O_y^2yH_1\cap F=\varnothing$. So a set $q_2(OxH_2)$ is a neighborhood of $x_2$ and $q_2(OxH_2)\cap \pi(F_1)= q_2(OxH_2)\cap q_2(FH_2)=\varnothing$. $\square$

Since $H_1$ is closed in $G$, the space $G/H_1$ is Hausdorff and we see that the map $\pi$ is perfect. So the space $G/H_1$ is compact by Theorem 3.7.2 from “General topology” by Ryszard Engelking (Heldermann Verlag, Berlin, 1989)).

enter image description here enter image description here

Alex Ravsky
  • 106,166