6

I was wondering if the following is correct:

Let $V=\bigoplus_{i\in\mathbb N}\mathbb Z$ and $R=\text{Hom}_{\ \mathbb Z}(V,V)$. Regard $R$ as an $R$-module. Then $R$ is free of rank $1$ with basis $\{\text{id}_{V}\}$. Now define a map $\phi$ as follows:

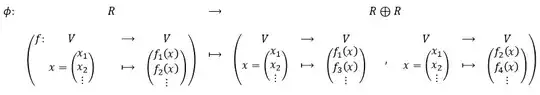Map \phi where $f_i: V \to \mathbb Z$ for each $f\in R$ are linear maps. Then $\phi$ is an isomorphism of $R$-modules.

Can I conclude as follows?

(1) Since $\phi$ is an isomorphism of $R$-modules we have $R\cong R^2$.

(2) Due to (1) we have $R^n\cong R^m$ for any $n,m\in\mathbb N$.

(3) Due to (2) we have that $R$ as an $R$-module is free of rank $k$ for any $k\in\mathbb N$.

Zev Chonoles
  • 132,937
Thomas
  • 165
  • 1
    Without sitting down to work out the details, my guess is that $\phi$ is a $\mathbb Z$-linear map but not an $R$-linear map. – Greg Martin Mar 02 '13 at 21:52

1 Answers1

0

The problem is, as Greg Martin guessed, that your $\phi$ is not $R$-linear. Let $1$ denote $\mathrm{id}_V\in R$, and $f\in R$ arbitrary, then $$\phi(f\cdot 1) \ne f\cdot \phi(1)\ .$$

user26857
  • 53,190
Berci
  • 92,013
  • Mhm, basically I was trying to find an explicit isomorphism for the following example: http://img42.imageshack.us/img42/9227/modulesi.jpg

    from https://www.math.lsu.edu/~adkins/m7211/AWchap3.pdf, see Remark 6.19 (2).

     – Thomas Mar 02 '13 at 23:03
  • Ok. I'm not that sure any more.. Have you verified my inequality statement? I might also have overlooked something.. – Berci Mar 03 '13 at 00:19
  • It seems that this answer shows that $\phi$ is indeed an isomorphism of $R$-modules. – user26857 Jan 09 '16 at 10:48
  • Moreover, I've checked your claim $\phi(f\cdot 1)\ne f\cdot\phi(f)$ and it seems to be wrong. – user26857 Jan 09 '16 at 10:50