0

In the following ODEs system: $$ \begin{array}{ll} \displaystyle \frac{d}{dt}u_1=-\lambda_1 u_1, \\ \displaystyle \frac{d}{dt}u_i=\lambda_{i-1}u_{i-1} -\lambda_i u_i, \quad i=2,\dots, N-1\\ \displaystyle \frac{d}{dt}u_N=\lambda_{N-1} u_{N-1}, \\ \end{array} $$ where $u_i=u_i(t)$, $\lambda_1,\dots,\lambda_{N-1}$ are positive constant. I have to prove that if $u_1(0)=u_1^0\geq 0,\dots u_N(0)=u_N^0\geq 0$ then the limits of this functions are $$ \lim_{t\to +\infty} u_i(t)=0, \quad i=1,\dots, N-1, $$ $$ \lim_{t\to +\infty} u_N(t)=C, $$ where $C=\sum_i u_i^0$.

It is clear that this is true for $u_1$ since I can solve the first equation. Then in the second equation the term $\lambda_1u_1$ goes to $0$ and in the limit, the second equation is similar to the first one, but this is only intuition. I want to find a rigorous proof. I have also try to find a Lyapunov function without success. Any hint?

davidivadful
  • 482
  • It is a linear system $X'=AX$. Thus all is determined by the eigen-decomposition of matrix $A$ (and, of course, initial conditions), with a triangular $A$. Have you this in your lecture notes ? – Jean Marie Apr 13 '19 at 10:56
  • I'm trying to apply all the results I know about exponential of a matrix and then writing the limit, but nothing works. Do you know a useful result in the case of a triangular matrix? – davidivadful Apr 13 '19 at 19:38
  • Passing the limit like you mentioned is perfectly rigorous. Just be a bit careful. – Paichu Apr 18 '19 at 04:27
  • @Paichu I think that the difficulty of the asker was to find a method for solving for example the second differential equation and prove that $u_2(t)\to 0$. Moreover "Just be a bit careful" could be said everywhere : it doesn't bring information. – Jean Marie Apr 18 '19 at 04:53

1 Answers1

1

Let us visualize the system in the case $N=5$ :

$$\begin{pmatrix}u'_1(t)\\ u'_2(t)\\ u'_3(t)\\ u'_4(t)\\ u'_5(t)\end{pmatrix}=\left(\begin{array}{rrrr|r}-\lambda_1&0&0&0&0\\\lambda_1&-\lambda_2&0&0&0\\0&\lambda_2&-\lambda_3&0&0\\0&0&\lambda_3&-\lambda_4&0\\ \hline 0&0&0&-\lambda_4&0\end{array}\right) \begin{pmatrix}u_1(t)\\u_2(t)\\u_3(t)\\u_4(t)\\u_5(t)\end{pmatrix}\tag{0}$$

with its solutions (Fig. 1) for a certain set of initial conditions :

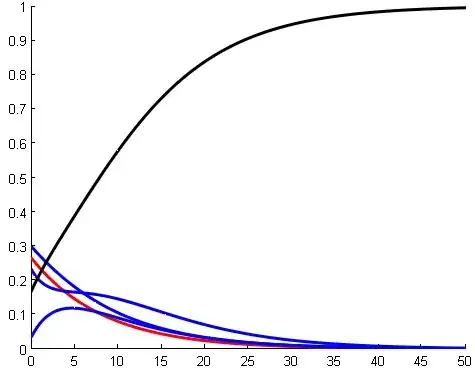
enter image description here

Fig. 1 : The $N=5$ curves of functions $u_k$ ; $u_1(t)=a e^{-\lambda_1 t}$ is figured in red. The curves for $u_2, u_3, u_4$ are in blue. The curve of $u_5$ (in black) has a particular horizontal asymptote y=C.

First remark : adding the $N$ diff. equations gives :

$$\left(\sum_{k=1}^N u_k\right)'=0,$$

whence

$$\sum_{k=1}^N u_k=C \ \ \text{(constant).}\tag{1}$$

Consider now the linear system $X'=AX$ obtained by leaving aside the $N$th differential equation.

$A$ being a $N-1 \times N-1$ triangular matrix (upper left block in (0)), its eigenvalues are the $-\lambda_k$s one finds on its diagonal.

Let us assume that all $\lambda_k$s are distinct (I think this hypothesis is reasonable).

Then $A$ is diagonalizable with $A=B\Lambda B^{-1}$, out of which $$\exp(tA)=B \exp(t \Lambda) B^{-1} \ = \ B \ \text{diag}(e^{- \lambda_k t})\ B^{-1} \to 0 \ \text{when} \ t \to \infty$$

(because all $\lambda_k$s are $>0$). As a consequence, whatever the vector $X(0)$ of initial conditions :

$$X(t)=\exp(tA)X(0) \to 0 \ \ \text{when} \ \ t \to \infty\tag{2}$$

As the coordinates of $X(t)$ are the $u_k(t)$, another way to state (2) is that

$$\lim_{t\to +\infty} u_k(t)=0, \quad k=1,\dots, N-1,\tag{3}$$

Now, using (1), we deduce from (3) that

$$\lim_{t\to +\infty} u_N(t)=C.$$

Remark : if some $\lambda_k$s are identical, we have to replace diagonalization $A=B\Lambda B^{-1}$ by a Jordan block decomposition. See for example the answer to How to calculate the matrix exponential explicitly for a matrix which isn't diagonalizable?

$\phantom{Here is the program}$

Jean Marie
  • 88,997
  • I have improved the presentation of my answer. Maybe, later on, I will include a solution using Laplace Transform. – Jean Marie Apr 18 '19 at 04:42