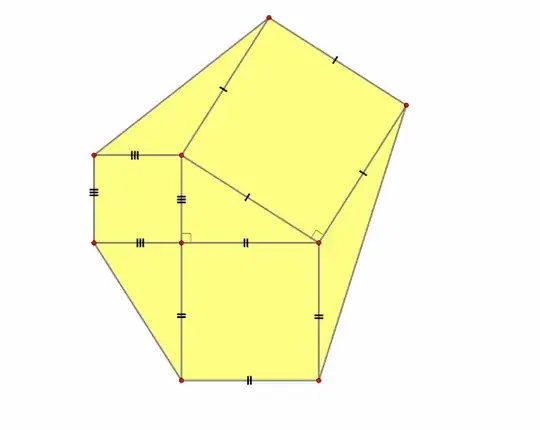
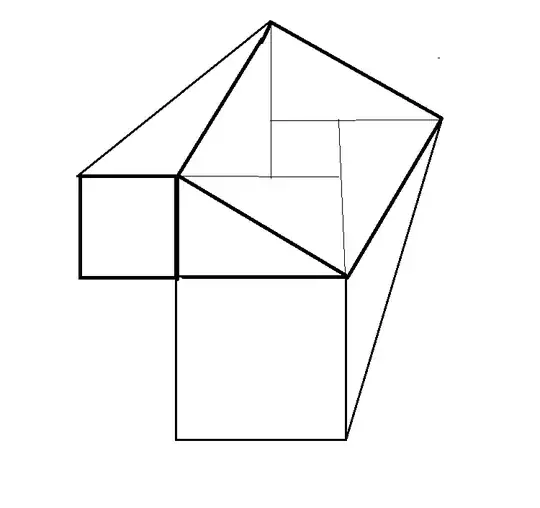
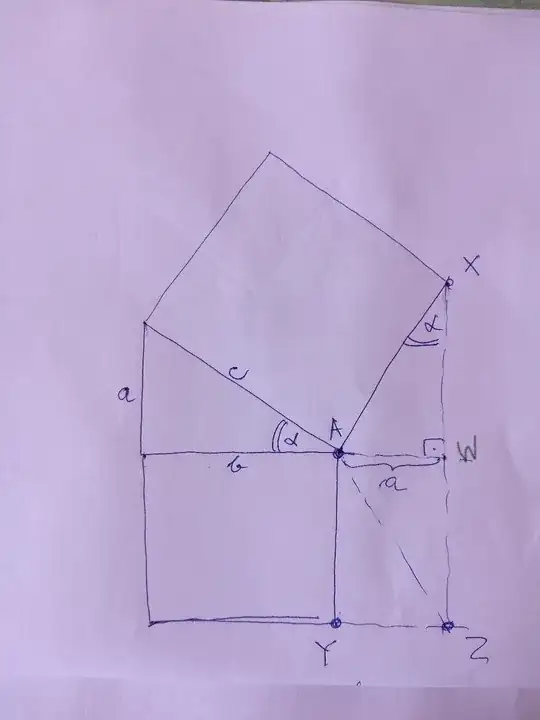
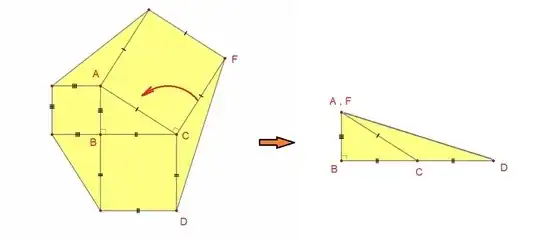
Here's the question: If the legs of the right triangle shown in the center of the figure have lengths a and b, find the area of the yellow region.
This is in terms of A and B. I'm particularly struggling to find how to find the areas of the non-right triangles.