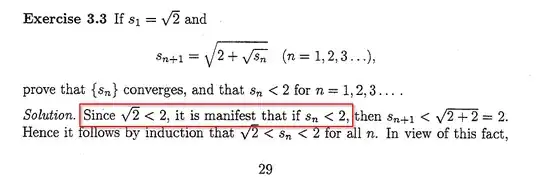1

I have an issue with solutions I've encountered to showing that sequence $\{s_n\}$ converges where $s_{n+1} = \sqrt{2 + \sqrt{s_n}}$

The question states: If $s_1 = \sqrt{2}$ and $s_{n+1} = \sqrt{2 + \sqrt{s_n}}$ for $n \in \mathbb{N}$ prove that $\{s_n\}$ converges and that $s_n < 2$ for $n \in \mathbb{N}$

In particular I have issue with the way this and another solution I saw went about getting the answer. The start of the solution is as follows:

enter image description here

If it specifically says I have to show $s_n < 2$ how are they allowed to all of a sudden use this "unknown fact" in establishing that the sequence is bounded? I get that it is a good way to then be able to apply the monotone convergence theorem, but it explicitly says to show this. I don't see how this constitutes making the proof sound.

D.C. the III
  • 5,719
  • 6
  • 53
  • 111
  • 1
    "How are they allowed to all of a sudden use this unknown fact in establishing that ...?" That's the main point of mathematical induction. – Andreas Blass Mar 29 '19 at 00:03

1 Answers1

3

$S_1<2$ is given, and $S_n<2 \implies S_{n+1} <2$. Thus, by induction, $S_n < 2 \;\; \forall n$.

Carl Schildkraut
  • 37,483
yona tan
  • 483