4

What is the IG length if the side of the square is 1? I wonder if it is half of the square side. The triangle below represents the haberdasher's problem.

version 2

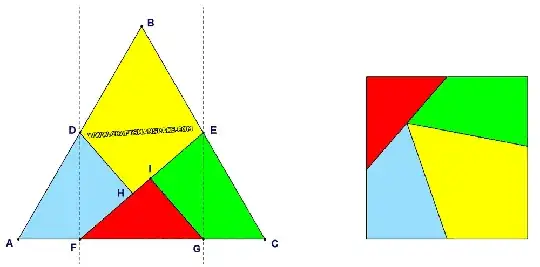
enter image description here

version 1 (added after edit, here the question is about JL)

enter image description here

The images are taken from here.

Edit. I posted two versions of the Dudeney triangle to square dissection. Original question was intended to concern the proper Dudeney dissection. It turned out that the version 2 is a dissection of equilateral triangle to rectangle, not a square. Though the rectangle is almost a square. Special thanks to SMM for revealing the truth.

Przemyslaw Remin
  • 51

2 Answers2

5

The upper side of the square is formed by $IG_{red}+IG_{green}=2IG$, because (as you can see below) the square is formed from the triangle by rotating the green piece by 180° about $G$, rotating the blue piece by 180° about $F$, and finally translating the yellow piece in place.

Hence you are right: IG is a half of the square side.

enter image description here

EDIT.

I copied below Dudeney's original construction (the second construction on that site is a fake). Suppose the side of the equilateral triangle is $2$, so that its altitude and its area are both $\sqrt3$. The side of the square is then $\root{4}\of3$.

In the construction (warning: the names of some points are different from those in the above diagram), $D$ and $E$ are midpoints of $AB$ and $BC$, while altitude $AE$ is produced to $F$ with $EF=EB=1$. It follows that the radius $AG$ of circle $AHF$ is $(\sqrt3+1)/2$. $BE$ is then produced to meet the circle at $H$. In right triangle $HEG$ we know that $GH=(\sqrt3+1)/2$ and $EG=AE-AG=(\sqrt3-1)/2$. From Pythagoras' theorem it follows then $EH=\root{4}\of3$, hence $EH$ is the same as the side of the square we want to construct.

Circle $HI$ is centered at $E$, hence $EI=EH=\root{4}\of3$. Let now $\alpha=\angle EIC$: by sine rule applied to triangle $EIC$ we have $$ \sin\alpha={\sin60°\cdot EC\over EI}={\root{4}\of3\over2}. $$ Point $J$ is then chosen such that $IJ=EC=1$ and $JL$ is perpendicular to $EI$. Hence $$JL=IJ\sin\alpha={\root{4}\of3\over2}$$ is exactly half side of the square.

enter image description here

You can read below a part of the article where Martin Gardner presented this problem: the construction given there is the same shown above. Gardner, in an addendum, also warns the reader that points $I$ and $J$ (figure above) are not exactly below $D$ and $E$.

enter image description here

Intelligenti pauca
  • 55,765
3

Denote by $a$ the side of the triangle. Since the areas of the triangle and the square are the same, we have $\frac{a^2\sqrt 3}{4}=1$, so $a=\frac{2}{\sqrt[4]3}$.

Set the coordinate system as follows: $A=(0,0)$, $C=(a,0)$ and $B=(\frac{a}{2},\frac{a\sqrt 3}{2})$. Then $D=\frac{A+B}{2}=(\frac{a}{4},\frac{a\sqrt 3}{4})$ and $E=\frac{C+B}{2}=(\frac{3a}{4},\frac{a\sqrt 3}{4})$. Further, by projecting $D$ and $E$, $F=(\frac{a}{4},0)$ and $G=(\frac{3a}{4},0)$.

We have $\vec{FE}=(\frac{a}{2},\frac{a\sqrt 3}{4})$, and $I=F+\alpha\vec{FE}=(\frac{a}{4}+\alpha\frac{a}{2},\alpha\frac{a\sqrt 3}{4})$ for some $\alpha$. Then $\vec{GI}= (\alpha\frac{a}{2}-\frac{a}{2},\alpha\frac{a\sqrt 3}{4})$. Since $FE\perp GI$ we have $\vec{FE}\cdot\vec{GI}=0$, so $\frac{a}{2}(\alpha\frac{a}{2}-\frac{a}{2})+ \frac{a\sqrt 3}{4}\alpha\frac{a\sqrt 3}{4}=0$, i.e. $\alpha-1+\frac{3}{4}\alpha=0$, where from $\alpha=\frac{4}{7}$.

So $\vec{GI}=(\frac{2a}{7}-\frac{a}{2},\frac{a\sqrt 3}{7})$. Therefore $GI^2=(\frac{2a}{7}-\frac{a}{2})^2+(\frac{a\sqrt 3}{7})^2= \frac{4a^2}{49}-\frac{2a^2}{7}+\frac{a^2}{4}+\frac{3a^2}{49}= \frac{a^2}{4}-\frac{a^2}{7}=\frac{3a^2}{28}$. Thus $GI=a\frac{\sqrt 3}{2\sqrt 7}= \frac{\sqrt[4]{3}}{\sqrt 7}$, and this is not $\frac{1}{2}$.

Edit. After Aretino posted his solution, which is correct, I started to wonder where is the mistake in mine. And there is no mistake. Mistake is in Version 2 of the construction. Namely, the rectangle obtained by Version 2 is not a square.

SMM
  • 4,579
  • 1
    It's awfully close, though, which explains OP's guess: It is approximately equal to $0.49743$. (I mean, assuming you've done your analysis correctly.) – Brian Tung Mar 26 '19 at 23:17
  • 1
    I agree. Version 2 of the construction method given in the OP's link, is wrong. – Jens Mar 27 '19 at 02:19
  • I appreciate your findings. Now I wonder if Aretino solution is correct. Aretino solution assumes that Dudeney was right proposing such dissection of equilateral triangle into square. After your answer the problem has become more puzzling then before I asked the question :-) – Przemyslaw Remin Mar 27 '19 at 10:16
  • @PrzemyslawRemin Aretino's solution shows how to transform an equilateral triangle into a rectangle, and $IG$ there is the half of one of the sides of the rectangle. Completely the same argument explains how you get square from the equilateral triangle if you consider Version 1 of the dissection. Version 2 is just wrong, the obtained rectangle is not a square. More generaly: if $D,E$ are midpoints of $BA,BC$, $F,G\in AC$ are such that $FG=a/2$ and $I,H$ are feet of the perpendiculars from $G,D$ on $FE$, then Aretino's argument shows how to build a rectangle from the obtained pieces. – SMM Mar 27 '19 at 13:24
  • @PrzemyslawRemin (Continuation.) Just the obtained rectangle is a square in a very special case, or a very special choice of $F$ and $G$, and this choice is described by Version 1. – SMM Mar 27 '19 at 13:27
  • @SMM Though I accepted Aretino's answer, I am very grateful for yours and I value it as much as Aretino's. You raised the puzzle to high level. Thank you. – Przemyslaw Remin Mar 28 '19 at 08:15