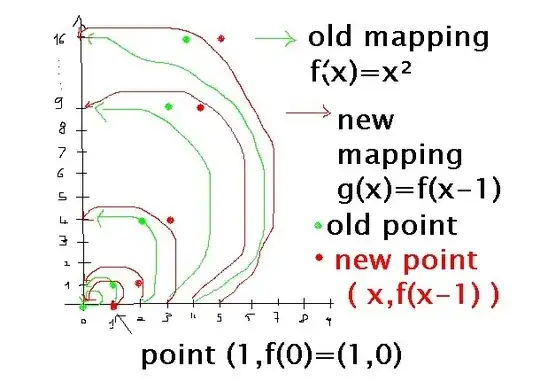
With the image below I try to explain in which way substituting (x-a) ( with a> 0) for x in the expression defining a function results in a shift to the right, although " intuition" tells us it should result in a shift to the left. To do this I use the auxiliary idea of "shifting" as "copying" or "imitating".
I would be interested in knowing whether this explanation could be efficient in the classroom at the high school level.
Suppose we have $y=f(x)=x^2$ and want to graph $y=g(x)=f(x-1).$
The function $g$ maps each $x$ to the image of $(x-1)$ under the function $f$.
In other words, each $x$ value has an "$ x-1$ " ( his own "$x-1$" ) , and copies his (x-1) 's image under the "old" mapping $f$ .
Since each "imitator" ( each $x$ value) is to the RIGHT of it's "model", that is it's " $x-1 $" , the change from the function $f(x)=x^2$ to the function $ g(x)=f(x-1)$ results , for each "old" point of the graph of f, in a translation of $1$ unit to the RIGHT.
Remark. - I first used the idea of " stealing" , for which I substitute the idea of " copying" or "imitating". I've just seen a post of Hyperpallium using the idea of " sampling" , even better.
Link to Hyperpallium's post : *Seeing* why horizontal shifts are reversed?