Snake lemma without elements – exactness

Question

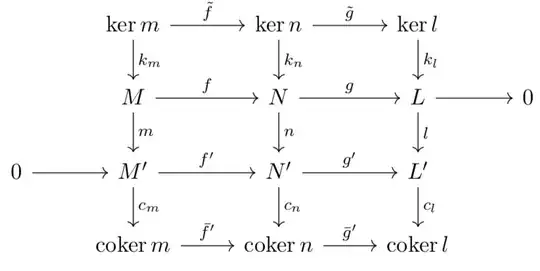
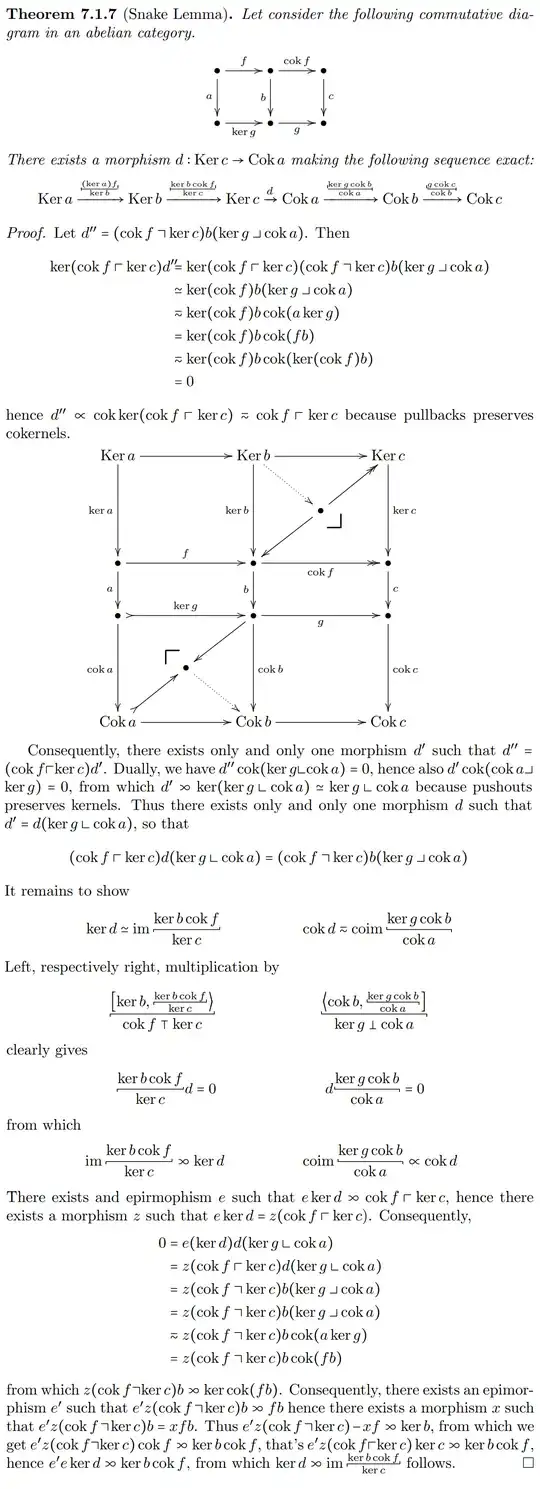
$\newcommand{\coker}{\operatorname{coker}}$ $\newcommand{\im}{\operatorname{im}}$ Consider the setup of the snake lemma with objects and morphisms as follows:

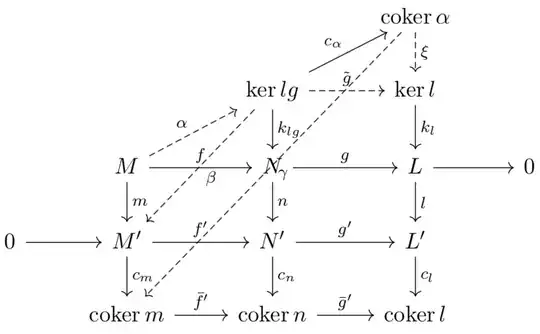
As mentioned in this answer, the connecting homomorphism $\ker l\to\coker m$ is constructed as follows:

• $lgk_lg=0$, so by the universal property of $\ker l$, the map $gk_{lg}$ factors through a morphism $\tilde g\colon\ker lg\to\ker l$.
• $g$ is epic. Applying left exactness of the kernel sequence (which we assume to be already shown) shows that $\tilde g$ and hence $\xi$ is epic. Question: why is $\xi$ an isomorphism?
• $k_l\tilde g\alpha=gf=0$, so by the universal property of $\coker\alpha$, the map $\tilde g$ factors through a morphism $\xi\colon\coker\alpha\to\ker l$.
• $lgf=0$, so by the universal property of $\ker lg$, the map $lg$ factors through a morphism $\alpha:M\to\ker lg$.
• $g'nk_{lg}=lgk_{lg}=0$, so by the universal property of $\ker g'$, the map $g'n$ factors through a morphism $\beta\colon\ker lg\to\ker g'=\im f'=M'$, where the latter equality holds because $f'$ is monic.
• $c_m\beta\alpha=c_mm=0$, so by the universal property of $\coker\alpha$, the map $c_m\beta$ factors through a map $\gamma\colon\coker\alpha\to\coker m$. The connecting homomorphism then is $\delta=\gamma\xi^{-1}$.

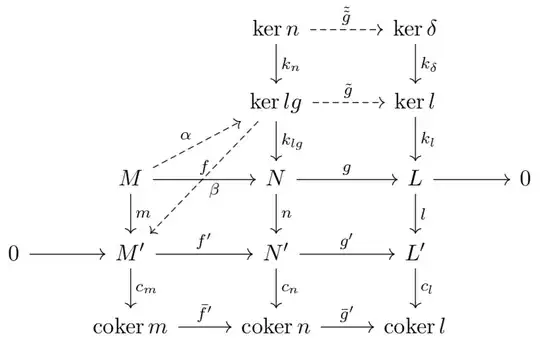
Now we want to show exactness at $\ker l$. From

One sees that:

• $lgk_n=g'nk_n=0$, so by the universal property of $\lg$, the map $\ker n\to N$ factors through a morphism $k_n\colon\ker n\to\ker lg$.
• $f'\beta k_n=nk_n=0$, so since $f'$ is monic, $\beta k_n=0$. Then $\delta \tilde gk_n=c_m\beta k_n=0$, so bt the universal property of $\ker\delta$, the map $\tilde gk_n$ factors through $\tilde{\tilde{g}}\colon\ker n\to\ker\delta$. This shows the one inclusion.

Question: I have no idea how to show surjectivity onto $\ker\delta$ of this factorisation. How do I do that?

Answer 1

Warning. This is a complete element-free proof of snake lemma in an abelian category taken from my personal notes. Sorry for the large image, but since heavly-non-standard notations are used I must to post a screenshot. I hope this can be useful, otherwise I will remove it.

Notations: If $f:X\to Y$ and $g:Y\to Z$, then $fg:X\to Z$ denote composition.

I write $f\propto g$ if there exists a morphism $h$ such that $f=gh$, while the reversed symbol of $\propto$ if there exists a morphism $h$ such that $f=hg$. If $f=hg$ with $g$ monic, then $h$ is uniquely determined and denoted with $\frac fg$. If $f=hg$ with $h$ an isomorphism, then I write $f\simeq g$.

If $f:X\to Z$ and $g:Y\to Z$ then $f\mathrel\urcorner g$ and $f\mathrel\ulcorner g$ denote pullback projections, so that $(f\mathrel\urcorner g)f=(f\mathrel\ulcorner g)g$.

If $f:Z\to X$ and $G:Z\to Y$ then $[f,g\rangle$ denote the morphism $Z\to X\times Y$ into the product. In particular, I write $f\mathrel\top g=[f\mathrel\urcorner g,f\mathrel\ulcorner g\rangle$.

Dual notions uses reversed symbols.