1

Question: find the eigenvalues and eigenfunctions of

$$y'' + \lambda y = 0, $$

with boundary conditions $y(0) + y'(0) = 0$ and $y(1)=0$.

I think I may be making an incredibly trivial error here, yet can't seem to spot it.

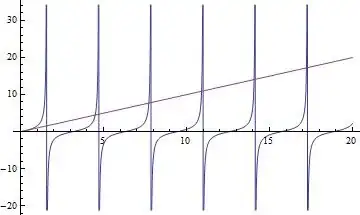
Assuming $\lambda=0$, we get $y(x) = c_1 + c_2\,x$. Differentiating, and using the boundary conditions, $(I)$ get $(2)$ equations, both of which say $c_1 + c_2 = 0$, i.e. $c_1 = -c_2$.

Having checked the answers, I have done it all right, except when using the boundary conditions, the answer I should get seems to be $y(x)= 1-x $, implying $c_1 = 1$, $c_2 = -1 $

Just wondering if another brain might be able to pick up my error !

Mhenni Benghorbal
  • 48,099
Sapph
  • 189

1 Answers1

0

You use the boundary conditions to determine $\lambda$. The general solution to the equation is

$$y(x) = A \cos{\sqrt{\lambda} x} + B \sin{\sqrt{\lambda} x}$$

The first condition at $x=0$ implies that

$$A + B \sqrt{\lambda} = 0$$

The other condition at $x=1$ implies that

$$A \cos{\sqrt{\lambda}} + B \sin{\sqrt{\lambda}} = 0$$

The combination of these two equations produces an equation for $\lambda$:

$$\tan{\sqrt{\lambda}} = \sqrt{\lambda}$$

The solution to the equation $\tan{y}=y$ for $y>0$ produces an infinite, yet discrete, set of solutions $y_n$ which are determined numerically. Here is a plot to help you visualize these solutions:

Plot of solutions of Tan(x) = x

The eigenvalues are then $\lambda_n = y_n^2$. Note that, for large $n$, the intersections are roughly at where $\tan{y}$ blows up; therefore, a good estimate of the eigenvalues for large $n$ is $\lambda_n \sim (n+3/2)^2 \pi^2$. The first few non-zero eigenvalues are $\lambda_1 \approx 20.2$, $\lambda_2 \approx 59.7$, and $\lambda_3 \approx 119$.

Now that we have the eigenvalues $\lambda_n$, we may determine the ratio of $A$ to $B$ to get the eigenfunctions $y_n(x)$ corresponding to the eigenvalues:

$$y_n(x) = A \left ( \cos{\sqrt{\lambda_n} x} - \frac{ \sin{\sqrt{\lambda_n} x}}{\sqrt{\lambda_n}}\right )$$

Ron Gordon
  • 141,538