Can there be two adjacent solid angles?

Question

Thanks for reading. My real question is the second part - in the first part I'm just explaining myself. Please read through! Thanks.

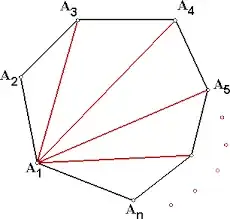
In 2D geometry, it is easy to picture what it means to add up 2 angles. For example, in this random picture I got off the internet, I can say that $\angle A_5A_1A_4 + \angle A_4A_1A_3 = \angle A_5A_1A_3$

However, with 3D geometry, I'm having trouble picturing what it would mean to add up two solid angles. If I'm adding up solid angles $A$ and $B$, I can't just draw the second angle $B$ so that it starts from the endpoint of $A$, as I could if it was in 2 Dimensions, because solid angles don't have a single endpoint.

So, how would I be able to picture 2 adjacent solid angles? Or 3 adjacent solid angles? Or does the idea of adjacency just not exist when we're considering solid angles?

The reason I'm asking is because I'm working on a proof that involves n arbitrary shape with a point somewhere within it. In order for my proof to work, I need to split up the shape's surface into pieces in such a way that the angle subtended by any section of a piece of the shape's surface relative to the point within the shape is equal for all pieces of that shape's surface.

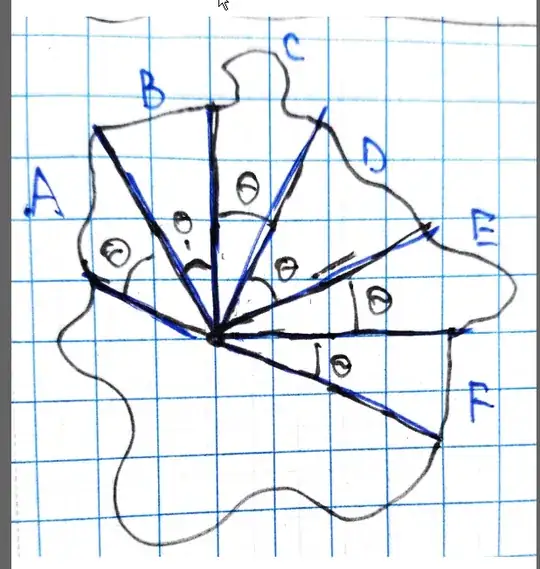
As you can see, the angle subtended by each piece of the shape's surface (with each piece denoted by a different letter) is the same for all the pieces of that shape's surface. They each subtend the angle $\theta$

So, so far my proof is working (kinda) for 2D. But I need it to apply to 3D.

But...how would I be able to do this in 3D? How would I be able to break up the 3D's shape surface into areas such that the angle (now a solid angle?) subtended by each section of that 3D shape's surface is equal for all the sections?

Thanks!!

---

Something else - when I break up the 3D shape into patches covering equal solid angles of its surface, I need all of the solid angles to be really small. Thanks!

Also, am I thinking of solid angles wrong? I haven't studied them explicitly (which I probably should soon) but have simply used them here and there when I've had to.

Answer 1

You should think of solid angles as surface patches on a given sphere of your choice (don't focus on the "cone" - which by the way isn't even a cone technically speaking - the "cone" is just trying to convey "3D-ness." Even for the cleanest surface patch on a sphere, the circle, the "3D cone" still isn't a cone rigorously speaking. For even more crazy surface patches on a sphere, something with crazy bends and sharp points in the boundary of the patch, the "cone" is even more warped). So just focus on the surface patch of your sphere.

Given 2 crazy surface patches anywhere on a common sphere, you might say that the 2 patches have adjacent solid angles if the boundaries of the patches share at least one point in common.

As a side note: angles and solid angles depend on where you place your circle and where you place your sphere (They don't depend on the size of the circle or the size of the sphere - just the placement). Draw some squiggly line on a sheet of paper. What angle does that squiggly line subtend? Depending on where you place your circle, you'll get different answers. For some circles, the angle subtended is close to $0$. Likewise for solid angles. Place a sphere in front of the meat of a sheet of paper (no matter the size of the sphere - you always get the same solid angle). Now look at the same sheet of paper on it's edge. The solid angle is $0$. The area traced out (projected) on a sphere is just a line, which has $0$ area.

As long as your object is closed, and the center of your sphere lies within the object, then the solid angle will be $4\pi$. This is easiest to see if the surface of the sphere is completely contained inside the object, or completely surrounds the object. For sphere's with their center within the object, but whose surface is partly within and partly without, the answer is still $4\pi$, and still fairly easy to see (Put your elbow at the center of the sphere. And point your arm/index finger to every point on the surface of the object of interest. The collection of rays which intersect the sphere's surface is the projected area on the sphere)

Answer 2

Solid angles don't have a shape, and this is confusing you. DWade64 explains it nicely. You can also do it the other way round. Imagine a beam of light from a point source placed inside an opaque spherical shell with a hole in it. Outside the shell this beam has a solid angle that is the area of the hole (Strictly, the area of the spherical cap that used to fill the hole) divided by the square of the radius of the sphere. It does not depend on the shape of the hole; it is proportional to the fraction of the light that escapes. Remove the shell entirely and the solid angle that fills of space is $4\pi$.

Calculating the solid angle in a general case is tricky. The easiest case is a 'spherical triangle', formed by three 'great circles'. These are circles whose centers are at the center of the sphere. If the angles at the three vertices are $\alpha, \beta,\gamma$ the area is $(\alpha+\beta+\gamma-\pi) R^2$. The sum of the angles of a spherical triangle are always greater than $\pi$ unless the triangle is very small.

A way to get eight triangles of equal area is to take your great circles as the equator plus two circles passing through the poles at right angles to each other. Each triangle then has a right angle at each vertex and its area is $3\times\pi/2-\pi=\pi/2$ which is one eighth of $4\pi$.

If you then split each triangle by the great circles that pass from each vertex to the mid-point of the opposite side you get 48 equal areas. But probably you want your solid angles to be arbitrarily small. Im not yet sure how to do that.

ADDENDUM

OK I see it now, but it may or may not help.

Take lines of latitude $\theta_0,\theta_1, \theta_2,..\theta_k,.. \theta_K,$ with $\theta_0=0,\theta_K=\pi/2$. Take lines of longitude with equal spacing $2\pi/M$. The area of a patch is

$$\frac{2\pi}{M}\int_{\theta_k}^{\theta_{k+1}}(2\pi R)(\sin{\theta}d\theta)= \frac{4\pi^2R^2}{M}(\cos{\theta_k}-\cos{\theta_{k+1}})$$ The patches will be of equal area if we take $$\theta_k=\cos^{-1}{k/K}$$